Документация

Создайте новый программный файл в редакторе. Этот файл будет содержать основную функцию и две локальных функции.

Задайте DDE первого порядка как локальную функцию.

function dydt = ddex1de(t,y,Z)
  ylag1 = Z(:,1);
  ylag2 = Z(:,2);
  dydt = [ylag1(1); ylag1(1)+ylag2(2); y(2)];
end

Задайте историю решения как локальную функцию.

function S = ddex1hist(t)
  S = ones(3,1);
end

Задайте задержки, τ1, …, τk в основной функции.

lags = [1,0.2];

Решите DDE путем вызова dde23 в основной функции. Передайте функцию DDE, задержки, историю решения и интервал интегрирования, [0,5], как входные параметры.

sol = dde23(@ddex1de,lags,@ddex1hist,[0,5]);

Функция dde23 производит непрерывное решение на целом интервале интегрирования [t0, _tf].

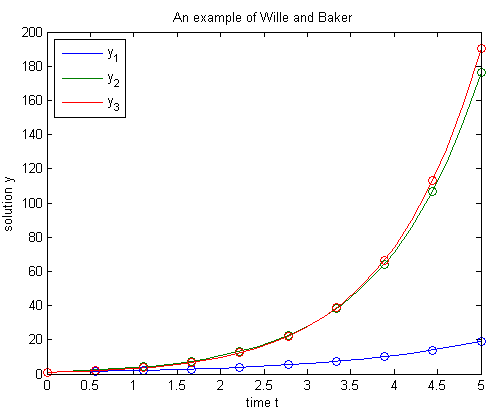
Постройте график решения, возвращенного dde23. Добавьте этот код к своей основной функции.

plot(sol.x,sol.y);
title('An example of Wille and Baker');
xlabel('time t');
ylabel('solution y');
legend('y_1','y_2','y_3','Location','NorthWest');

Оцените решение в 10 равномерно распределенных точках на интервале интегрирования. Затем постройте график результатов на тех же осях как sol.y y. Добавьте этот код к основной функции.

tint = linspace(0,5,10);
Sint = deval(sol,tint)
hold on
plot(tint,Sint,'o');

Запустите свою программу, чтобы сгенерировать и построить график результатов.