Интерполяция является методом для оценки значения в местоположении запроса, которое находится в области набора демонстрационных точек данных. Демонстрационный набор данных, заданный местоположениями X и соответствующие значения V, может быть интерполирован, чтобы произвести функцию формы V = F (X). Эта функция может затем использоваться, чтобы оценить точку запроса Xq, дать Vq = F (Xq). Это - однозначная функция; для любого запроса Xq в области X это произведет уникальное значение Vq. Демонстрационные данные приняты, чтобы уважать это свойство в порядке произвести удовлетворительную интерполяцию. Еще одна интересная характеристика - то, что функция интерполяции проходит через точки данных. Это - важное различие между подбором кривой кривой/поверхности и интерполяцией. В подборе кривой функция не обязательно проходит через демонстрационные точки данных.
Вычисление значения Vq обычно основано на точках данных в окружении точки запроса Xq. Существуют многочисленные подходы к выполнению интерполяции. В MATLAB® интерполяция классифицируется в две категории в зависимости от структуры демонстрационных данных. Демонстрационные данные могут быть заказаны в выровненной осью сетке, или они могут быть рассеяны. В случае распределения с координатной сеткой точек выборки можно усилить организованную структуру данных, чтобы эффективно найти точки выборки в окружении запроса. Интерполяция данных, имеющий разброс, с другой стороны, требует триангуляции точек данных, и это представляет дополнительный уровень вычисления.
Два подхода к интерполяции покрыты следующими разделами:
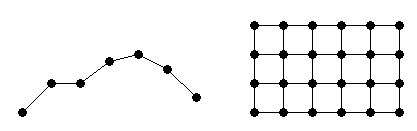
Раздел Interpolating Gridded Data покрывает 1D интерполяцию и N-D (N ≥ 2) интерполяция демонстрационных данных в выровненном осью формате сетки:
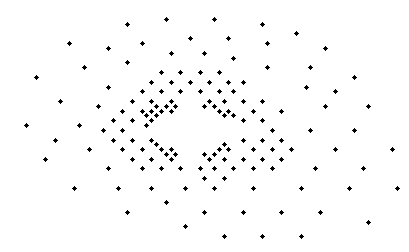
Раздел Interpolating Scattered Data покрывает N-D (N ≥ 2) интерполяция данных, имеющий разброс: