Совместимые размеры массивов для основных операций

Большая часть двоичного файла (двух-входной параметр), операторы и функции в ^MATLAB® поддерживают числовые массивы, которые имеют совместимые размеры. Два входных параметра имеют совместимые размеры, если для каждой размерности размеры размерности входных параметров являются или тем же самым или одним из них, 1. В самых простых случаях два размера массивов совместимы, если они - точно то же самое или если вы - скаляр. MATLAB неявно расширяет массивы с совместимыми размерами, чтобы быть одного размера во время выполнения поэлементной операции или функции.

Вводы с совместимыми размерами

2D Вводы

Это некоторые комбинации скаляров, векторов и матриц, которые имеют совместимые размеры:

Два входных параметра, которые являются точно тем же размером.
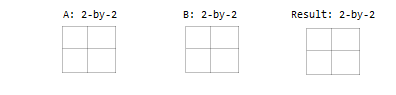
Один входной параметр является скаляром.
Один входной параметр является матрицей, и другой вектор - столбец с тем же количеством строк.
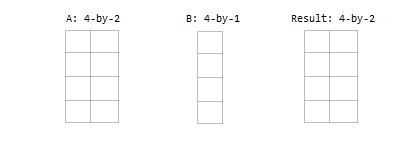
Один входной параметр является вектором - столбцом, и другой вектор - строка.

Многомерные массивы

Каждый массив в MATLAB имеет последующие измерения размера 1. Для многомерных массивов это означает, что матрица 3 на 4 совпадает с матрицей размера 3 4 1 1 на 1. Примеры многомерных массивов с совместимыми размерами:

Один входной параметр является матрицей, и другой трехмерный массив с тем же количеством строк и столбцов.
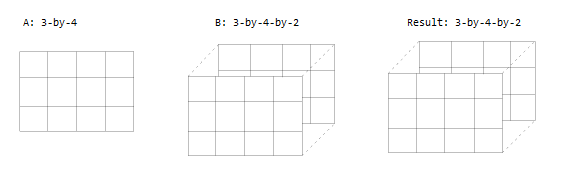
Один входной параметр является матрицей, и другой трехмерный массив. Размерности - все или то же самое или один из них - 1.

Пустые массивы

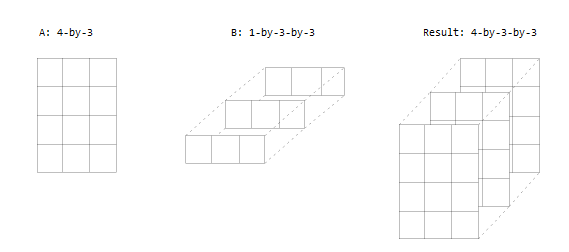
Правила являются тем же самым для пустых массивов или массивов, которые имеют размер размерности нуля. Размер размерности, которая не равна 1, определяет размер вывода. Это означает, что размерности с размером нуля должны быть соединены с размерностью размера 1 или 0 в другом массиве, и что вывод имеет размер размерности 0.

     A: 1-by-0     
     B: 3-by-1
Result: 3-by-0

Вводы с несовместимыми размерами

Несовместимые входные параметры имеют размеры, которые не могут быть неявно расширены, чтобы быть одного размера. Например:

Один из размеров размерности не равен, и ни один не равняется 1.
```
A: 3-by-2
B: 4-by-2
```
Два нескалярных вектора - строки с длинами, которые не являются тем же самым.
```
A: 1-by-3
B: 1-by-4
```

Примеры

Вычитание вектора из матрицы

Чтобы упростить векторные операции над матрицей, используйте неявное расширение с размерными функциями, такими как sum, mean, min и другие.

Например, вычислите среднее значение каждого столбца в матрице, затем вычтите среднее значение из каждого элемента.

A = magic(3)

A =

     8     1     6
     3     5     7
     4     9     2

C = mean(A)

C =

     5     5     5

A - C

ans =

     3    -4     1
    -2     0     2
    -1     4    -3

Добавление вектора строки и столбца

Векторы строки и столбца имеют совместимые размеры, и когда вы выполняете операцию на них, результатом является матрица.

Например, добавьте вектор строки и столбца. Результат совпадает с bsxfun(@plus,a,b).

a = [1 2 3 4]

ans =

     1     2     3     4

b = [5; 6; 7]

a + b

ans =

     6     7     8     9
     7     8     9    10
     8     9    10    11

Смотрите также

bsxfun

Документация