Прямое сквозное соединение означает, что выводом (или переменная частота дискретизации для переменных блоков частоты дискретизации) управляет непосредственно значение сигнала входного порта. Как правило, порт S-входного-параметра-функции имеет прямое сквозное соединение если
Выходная функция (mdlOutputs) является функцией входного параметра u. Таким образом, существует прямое сквозное соединение, если к входному параметру u получает доступ mdlOutputs. Выходные параметры могут также включать выводы графических данных, как в случае осциллографа Графика XY.
“Время следующего хита” функция (mdlGetTimeOfNextVarHit) переменной S-функции частоты дискретизации получает доступ к входному параметру u.
Пример системы, которая требует ее входных параметров (то есть, имеет прямое сквозное соединение), операция
где u является входным параметром, k является усилением, и y является вывод.
Пример системы, которая не требует ее входных параметров (то есть, не имеет прямого сквозного соединения), алгоритм простой интеграции
где x является состоянием, является производной состояния относительно времени, u является входным параметром, и y является вывод. Simulink® интегрирует переменную
Очень важно установить прямой флаг сквозного соединения правильно, потому что это влияет на порядок выполнения блоков в вашей модели и используется, чтобы обнаружить алгебраические циклы (см. Алгебраические Циклы в Использовании Simulink). Если результаты симуляции для модели, содержащей вашу S-функцию, не сходятся, или сбои моделирования, у вас может быть прямой набор флага сквозного соединения неправильно. Попытайтесь включить прямой флаг сквозного соединения и установить Алгебраическую диагностику решателя цикла на warning (см. Алгебраическую опцию цикла на Образцовых Параметрах конфигурации: страница с описанием Диагностики в Графическом интерфейсе пользователя Simulink). Впоследствии выполнение моделирования отображает любые алгебраические циклы в модели и показывает, поместил ли механизм вашу S-функцию в алгебраическом цикле.
Можно записать S-функцию, чтобы поддержать произвольные входные размерности. В этом случае механизм Simulink определяет фактические входные размерности, когда моделирование запускается путем оценки размерностей входных векторов, управляющих S-функцией. Ваша S-функция может также использовать входные размерности, чтобы определить количество непрерывных состояний, количество дискретных состояний и количество выходных параметров.
Динамически размерный входной параметр может иметь различный размер для каждого экземпляра S-функции в конкретной модели или во время различных моделирований, однако входной размер каждого экземпляра S-функции статичен в течение конкретного моделирования.
S-функция MEX C и S-функция Level 2 MATLAB® могут иметь несколько портов ввода и вывода, и каждый порт может иметь различные размерности. Количество размерностей и размер каждой размерности могут быть определены динамически.
Например, следующая иллюстрация показывает два экземпляра того же Блока s-function в модели.
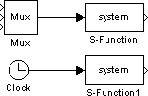
Верхний Блок s-function управляется блоком с трехэлементным выходным вектором. Более низкий Блок s-function управляется блоком со скалярным выводом. Путем указывания, что Блок s-function динамически измерил входные параметры, та же S-функция может разместить обе ситуации. Механизм Simulink автоматически вызывает блок с соответственно размерным входным вектором. Точно так же, если другие блочные характеристики, такие как количество выходных параметров или количество дискретных или непрерывных состояний, заданы так же динамически измеренные, механизм задает эти векторы, чтобы быть той же длиной как входной вектор.
Смотрите Порты Ввода и вывода для получения дополнительной информации о конфигурировании S-входного-параметра-функции и выходных портов.
И Уровень 2, MATLAB и S-функции MEX C предоставляют следующие возможности частоты дискретизации, которые допускают высокую степень гибкости в определении, когда S-функция выполняется:
Время непрерывной выборки — Для S-функций, которые имеют непрерывные состояния и/или не выбрали нулевые пересечения (видит Фазы Моделирования в Динамических системах для объяснения нулевых пересечений). Для этого типа S-функции вывод изменяется в незначительных временных шагах.
Непрерывный, но зафиксированный в незначительной частоте дискретизации временного шага — Для S-функций, которые должны выполниться на каждом главном шаге моделирования, но не изменять значение во время незначительных временных шагов.
Дискретная частота дискретизации — Если поведение вашей S-функции является функцией интервалов дискретного времени, можно задать частоту дискретизации, чтобы управлять, когда механизм Simulink вызывает S-функцию. Можно также задать смещение, которое задерживает каждый хит частоты дискретизации. Значение смещения не может превысить соответствующую частоту дискретизации.
Хит частоты дискретизации происходит во временных стоимостях, определенных формулой
TimeHit = (n * period) + offset
где целочисленный n является текущим шагом моделирования. Первое значение n всегда является нулем.
Если вы задаете дискретную частоту дискретизации, механизм вызывает S-функцию mdlOutputs и стандартные программы mdlUpdate при каждом хите частоты дискретизации (как задано в предыдущем уравнении).
Переменная частота дискретизации — дискретная частота дискретизации, где интервалы между демонстрационными хитами могут отличаться. В начале каждого шага моделирования S-функции с переменными частотами дискретизации запрошены в течение времени следующего хита.
Наследованная частота дискретизации — Иногда S-функция не имеет никаких свойственных характеристик частоты дискретизации (то есть, это или непрерывно или дискретно, в зависимости от частоты дискретизации некоторого другого блока в системе). В этом случае можно указать, что частота дискретизации наследована. Простым примером этого является блок Gain, который наследовал его частоту дискретизации от блока, управляющего им.
S-функция может наследовать свою частоту дискретизации от
Ведущий блок
Целевой блок
Самая быстрая частота дискретизации в системе
Задавать частоту дискретизации S-функции наследовано, используйте-1 на Уровне 2 S-функции MATLAB и INHERITED_SAMPLE_TIME в S-функциях MEX C как частота дискретизации. Для получения дополнительной информации о распространении частот дискретизации смотрите, Как Распространение Влияет на Наследованные Частоты дискретизации в Руководстве пользователя Simulink.
S-функции могут быть или синглом или мультиуровнем; S-функция мультиуровня имеет несколько частот дискретизации.
Частоты дискретизации заданы в парах в этом формате: [sample_time, offset_time].
Допустимые пары частоты дискретизации для S-функции MEX C
[CONTINUOUS_SAMPLE_TIME, 0.0] [CONTINUOUS_SAMPLE_TIME, FIXED_IN_MINOR_STEP_OFFSET] [discrete_sample_time_period, offset] [VARIABLE_SAMPLE_TIME, 0.0]
где
CONTINUOUS_SAMPLE_TIME = 0.0 FIXED_IN_MINOR_STEP_OFFSET = 1.0 VARIABLE_SAMPLE_TIME = -2.0
и имена переменных курсивом указывают, что действительное значение требуется.
Также можно указать, что частота дискретизации наследована от ведущего блока. В этом случае S-функция MEX C имеет только одну пару частоты дискретизации, также
[INHERITED_SAMPLE_TIME, 0.0]
или
[INHERITED_SAMPLE_TIME, FIXED_IN_MINOR_STEP_OFFSET]
где
INHERITED_SAMPLE_TIME = -1.0
Допустимые пары частоты дискретизации для Уровня 2 S-функция MATLAB
[0 offset] % Continuous sample time [discrete_sample_time_period, offset] % Discrete sample time [-1, 0] % Inherited sample time [-2, 0] % Variable sample time
где имена переменных курсивом указывают, что действительное значение требуется. При использовании времени непрерывной выборки offset 1 указывает, что вывод фиксируется в незначительных временных шагах интегрирования. offset 0 указывает на выходные изменения на каждом незначительном временном шаге интегрирования.
Используйте следующие инструкции для справки с определением частот дискретизации:
Непрерывная S-функция, которая изменяется во время незначительных этапов интеграции, должна указать [CONTINUOUS_SAMPLE_TIME, 0.0] частота дискретизации.
Непрерывная S-функция, которая не изменяется во время незначительных этапов интеграции, должна указать частоту дискретизации [CONTINUOUS_SAMPLE_TIME, FIXED_IN_MINOR_STEP_OFFSET].
Дискретная S-функция, которая изменяется на заданном уровне, должна указать дискретную пару частоты дискретизации, [discrete_sample_time_period, offset], где
discrete_sample_period > 0.0
и
0.0 ≤ offset < discrete_sample_period
Дискретная S-функция, которая изменяется по плавающему курсу, должна указать переменный шаг дискретная частота дискретизации.
[VARIABLE_SAMPLE_TIME, 0.0]
В S-функции MEX C стандартная программа mdlGetTimeOfNextVarHit называется, чтобы получить время следующего демонстрационного хита для переменного шага дискретная задача. На Уровне 2 S-функция MATLAB свойство NextTimeHit собирается в методе Outputs установить следующий демонстрационный хит.
Если ваша S-функция не имеет никакой внутренней частоты дискретизации, необходимо указать то время дискретизации, наследован. Существует два случая:
S-функция, которая изменяется как ее входной параметр изменения, даже во время незначительных этапов интеграции, должна указать частоту дискретизации [INHERITED_SAMPLE_TIME, 0.0].
S-функция, которая изменяется как ее входной параметр, изменяется, но не изменяется во время незначительных этапов интеграции (то есть, остается фиксированным во время незначительных временных шагов), должен указать частоту дискретизации [INHERITED_SAMPLE_TIME, FIXED_IN_MINOR_STEP_OFFSET].
Блок Scope является хорошим примером этого типа блока. Этот блок запускается по курсу его ведущего блока, или непрерывного или дискретного, но никогда не запускается на незначительных шагах. Если бы это сделало, отображение осциллографа показало бы промежуточные вычисления решателя, а не конечного результата в каждом моменте времени.
Смотрите Задают Частоты дискретизации S-функции для получения информации о реализации различных типов частот дискретизации в S-функциях.
Уровень 2 S-функция MATLAB | Функция MATLAB | S-функция | Разработчик S-функции