Квантование в разделе Quantizing a Signal не требует никакого априорного знания о переданном сигнале. На практике можно часто высказывать образованные предположения о существующем сигнале на основе прошлых передач сигнала. Используя такие образованные предположения, чтобы помочь квантовать сигнал известен как прогнозирующее квантование. Наиболее распространенный прогнозирующий метод квантования является дифференциальной импульсной модуляцией кода (DPCM).
Функции dpcmenco, dpcmdeco и dpcmopt могут помочь вам реализовать прогнозирующий квантизатор DPCM с линейным предиктором.
Чтобы определить энкодер для такого квантизатора, необходимо предоставить не, только раздел и книга шифров, как описано в Представляют Разделы и Представляют Книги шифров, но также и предиктор. Предиктор является функцией, что использование энкодера DPCM, чтобы произвести образованное предполагает каждый шаг. Линейный предиктор имеет форму
y(k) = p(1)x(k-1) + p(2)x(k-2) + ... + p(m-1)x(k-m+1) + p(m)x(k-m)
где x является исходным сигналом, y(k) пытается предсказать значение x(k), и p является m - кортеж вещественных чисел. Вместо того, чтобы квантовать сам x, энкодер DPCM квантует прогнозирующую ошибку, x-y. Целочисленный m выше называется прогнозирующим порядком. Особый случай, когда m = 1 называется модуляцией дельты.
Если предположение для k th значение x сигнала, на основе более ранних значений x,
y(k) = p(1)x(k-1) + p(2)x(k-2) +...+ p(m-1)x(k-m+1) + p(m)x(k-m)
затем соответствующий вектор предиктора для функций тулбокса
predictor = [0, p(1), p(2), p(3),..., p(m-1), p(m)]
Начальный нуль в векторе предиктора целесообразен, если вы просматриваете вектор как полиномиальную передаточную функцию фильтра конечного импульсного ответа (FIR).
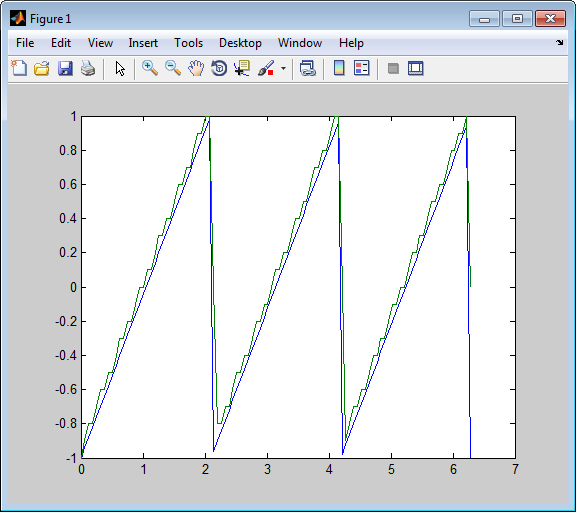
Простой особый случай DPCM квантует различие между текущим значением сигнала и его значением на предыдущем шаге. Таким образом предиктором является только y(k) = x (k - 1). Код ниже реализует эту схему. Это кодирует пилообразное сообщение, декодирует его и строит обоих исходные и декодируемые сигналы. Сплошная линия является исходным сигналом, в то время как пунктирная линия является восстановленными сигналами. Пример также вычисляет среднеквадратичную погрешность между исходными и декодируемыми сигналами.
predictor = [0 1]; % y(k)=x(k-1) partition = [-1:.1:.9]; codebook = [-1:.1:1]; t = [0:pi/50:2*pi]; x = sawtooth(3*t); % Original signal % Quantize x using DPCM. encodedx = dpcmenco(x,codebook,partition,predictor); % Try to recover x from the modulated signal. decodedx = dpcmdeco(encodedx,codebook,predictor); plot(t,x,t,decodedx,'--') legend('Original signal','Decoded signal','Location','NorthOutside'); distor = sum((x-decodedx).^2)/length(x) % Mean square error
Вывод
distor =
0.0327
Раздел Optimize Quantization Parameters описывает, как использовать данные тренировки с функцией lloyds, чтобы помочь найти параметры квантования, которые минимизируют искажение сигнала.
В этом разделе описываются подобные процедуры для использования функции dpcmopt в сочетании с двумя функциями dpcmenco и dpcmdeco, которые сначала появляются в предыдущем разделе.
Данные тренировки, которые вы используете с dpcmopt, должны быть типичны для видов сигналов, которые вы будете на самом деле квантовать с dpcmenco.
Этот пример подобен тому в последнем разделе. Однако, где последний пример создал predictor, partition и codebook прямым, но случайным способом, этот пример использует ту же книгу шифров (теперь названный initcodebook) как исходное предположение для нового оптимизированного параметра книги шифров. Этот пример также использует прогнозирующий порядок, 1, как желаемый порядок нового оптимизированного предиктора. Функция dpcmopt создает эти оптимизированные параметры, с помощью пилообразного x сигнала в качестве данных тренировки. Пример продолжает квантовать данные тренировки сам; в теории оптимизированные параметры подходят для квантования других данных, которые подобны x. Заметьте, что среднеквадратическое искажение здесь намного меньше, чем искажение в предыдущем примере.
t = [0:pi/50:2*pi]; x = sawtooth(3*t); % Original signal initcodebook = [-1:.1:1]; % Initial guess at codebook % Optimize parameters, using initial codebook and order 1. [predictor,codebook,partition] = dpcmopt(x,1,initcodebook); % Quantize x using DPCM. encodedx = dpcmenco(x,codebook,partition,predictor); % Try to recover x from the modulated signal. decodedx = dpcmdeco(encodedx,codebook,predictor); distor = sum((x-decodedx).^2)/length(x) % Mean square error
Вывод
distor =
0.0063