Это тематическое исследование демонстрирует инструменты для классической системы управления путем продвижения через проект демпфера отклонения от курса для 747® реактивный транспортный самолет.
Струйная модель во время рейса круиза в МАХЕ = 0.8 и H = 40 000 футов
A=[-.0558 -.9968 .0802 .0415;
.598 -.115 -.0318 0;
-3.05 .388 -.4650 0;
0 0.0805 1 0];
B=[ .00729 0;
-0.475 0.00775;
0.153 0.143;
0 0];
C=[0 1 0 0;
0 0 0 1];
D=[0 0;
0 0];
sys = ss(A,B,C,D);Следующие команды задают эту модель в пространстве состояний как объект LTI и присоединяют имена к состояниям, входным параметрам и выходным параметрам.
states = {'beta' 'yaw' 'roll' 'phi'};
inputs = {'rudder' 'aileron'};
outputs = {'yaw' 'bank angle'};
sys = ss(A,B,C,D,'statename',states,...
'inputname',inputs,...
'outputname',outputs);
Можно отобразить модель LTI sys путем ввода sys. Эта команда приводит к следующему результату.
a =
beta yaw roll phi
beta -0.0558 -0.9968 0.0802 0.0415
yaw 0.598 -0.115 -0.0318 0
roll -3.05 0.388 -0.465 0
phi 0 0.0805 1 0
b =
rudder aileron
beta 0.00729 0
yaw -0.475 0.00775
roll 0.153 0.143
phi 0 0
c =
beta yaw roll phi
yaw 0 1 0 0
bank angle 0 0 0 1
d =
rudder aileron
yaw 0 0
bank angle 0 0
Continuous-time model.Модель имеет два входных параметров и два выходных параметров. Модули являются радианами для beta (угол заноса) и phi (угол банка) и радианами/секунда для yaw (уровень отклонения от курса) и roll (уровень списка). Руководящий принцип и отклонения элерона исчисляются в радианах также.
Вычислите полюса разомкнутого цикла и постройте их в s - плоскость.
>> damp(sys)
Pole Damping Frequency Time Constant
(rad/seconds) (seconds)
-7.28e-03 1.00e+00 7.28e-03 1.37e+02
-5.63e-01 1.00e+00 5.63e-01 1.78e+00
-3.29e-02 + 9.47e-01i 3.48e-02 9.47e-01 3.04e+01
-3.29e-02 - 9.47e-01i 3.48e-02 9.47e-01 3.04e+01
pzmap(sys)
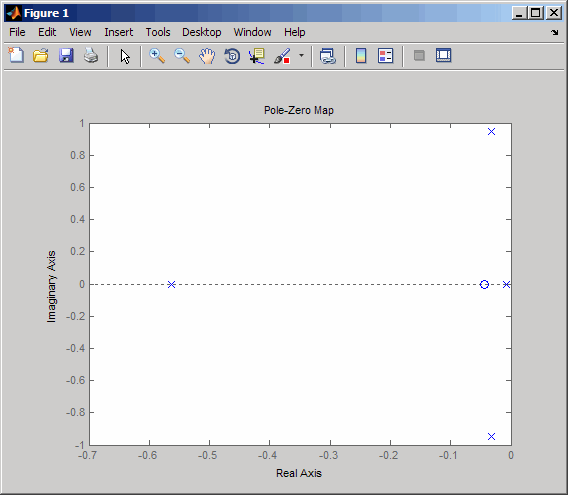
Эта модель имеет одну пару слегка ослабленных полюсов. Они соответствуют тому, что называется "режимом Голландского шага".
Предположим, что вы хотите разработать компенсатор, который увеличивает затухание этих полюсов, так, чтобы получившиеся комплексные полюса имели отношение затухания ζ> 0.35 с собственной частотой ωn <1 рад/секунда. Можно сделать это использование аналитических инструментов Control System Toolbox™.
Во-первых, выполните некоторый анализ разомкнутого цикла, чтобы определить возможные стратегии управления. Запустите с ответа времени (вы могли использовать step или impulse здесь).
impulse(sys)
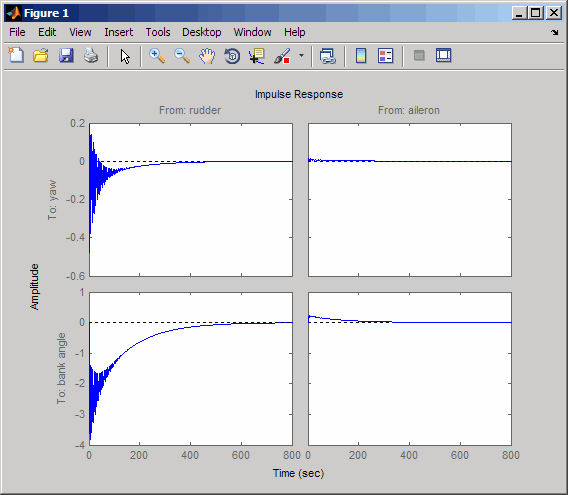
Импульсный ответ подтверждает, что система слегка ослабляется. Но период времени слишком долог, потому что пассажиры и пилот более обеспокоены поведением в течение первых нескольких секунд, а не первых нескольких минут. Затем посмотрите на ответ за меньший период времени 20 секунд.
impulse(sys,20)
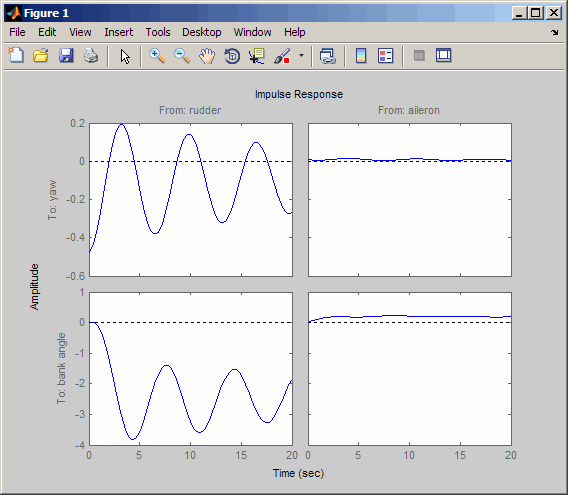
Посмотрите на график от элерона (введите 2) к углу банка (выводит 2). Чтобы показать только этот график, щелкните правой кнопкой и выберите I/O Selector, затем нажмите (2,2) запись. Селектор ввода-вывода должен выглядеть так.
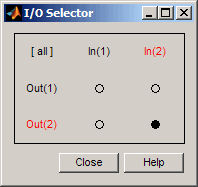
Новую фигуру показывают ниже.
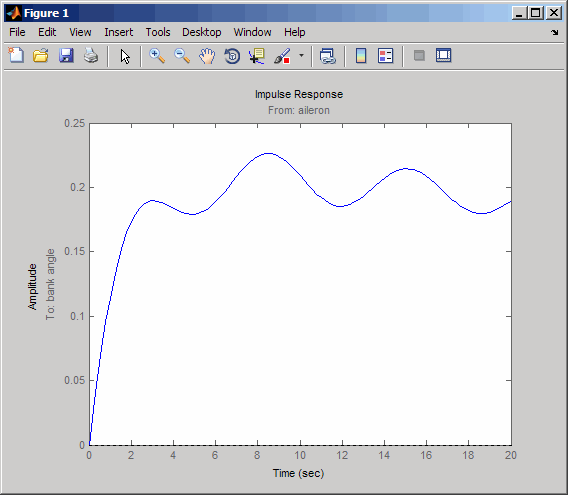
Самолет колеблется вокруг ненулевого угла банка. Таким образом самолет поворачивается в ответ на импульс элерона. Это поведение окажется важным позже в этом тематическом исследовании.
Как правило, демпферы отклонения от курса разработаны с помощью уровня отклонения от курса, как обнаружено выведено и руководящего принципа как вход управления. Посмотрите на соответствующую частотную характеристику.
sys11=sys('yaw','rudder') % Select I/O pair.
bode(sys11)
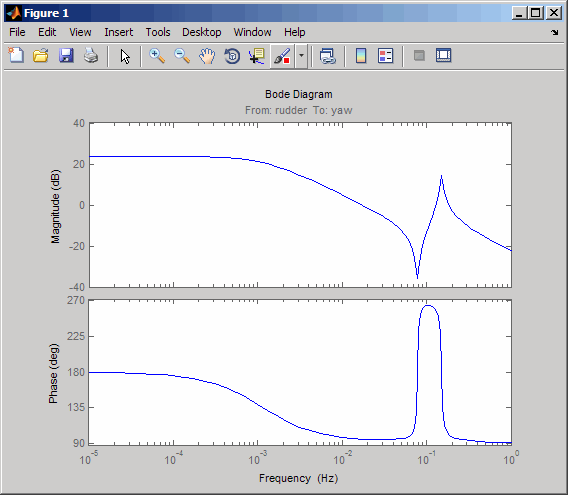
От этой диаграммы Боде вы видите, что руководящий принцип имеет значительный эффект вокруг слегка ослабленного режима Голландского шага (то есть, рядом ω = 1 рад/секунда).
Разумная цель проекта состоит в том, чтобы обеспечить порцию затухания ζ> 0.35 с собственной частотой ωn <1,0 рада/секунда. Поскольку самый простой компенсатор является статическим усилением, сначала попытайтесь определить соответствующие значения усиления с помощью метода корневого годографа.
% Plot the root locus for the rudder to yaw channel rlocus(sys11)
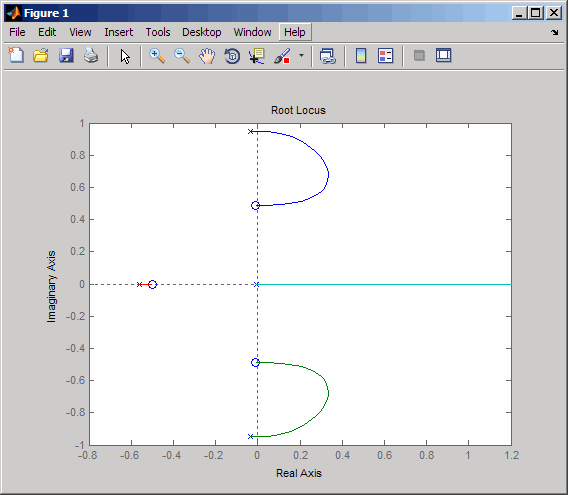
Это - корневой годограф для отрицательной обратной связи и показывает, что система идет нестабильная почти сразу. Если, вместо этого, вы используете позитивные отклики, можно смочь сохранить стабильность системы.
rlocus(-sys11) sgrid
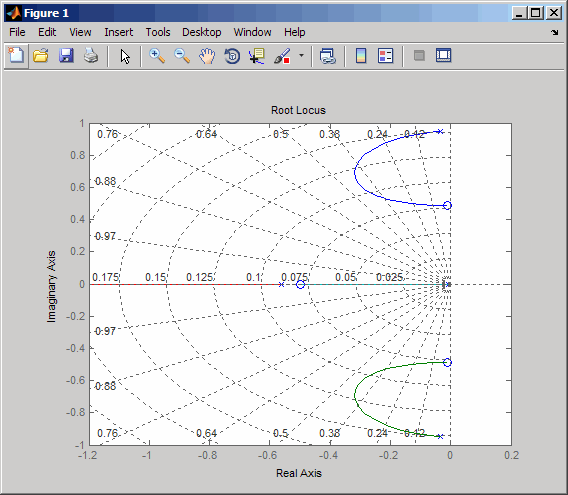
Это выглядит лучше. При помощи простой обратной связи можно достигнуть отношения затухания ζ> 0.45. Нажмите на синюю кривую и переместите маркер данных, чтобы отследить значения затухания и усиление. Чтобы достигнуть 0,45 отношений затухания, усиление должно быть приблизительно 2,85. Эти данные показывают маркер данных с подобными значениями.
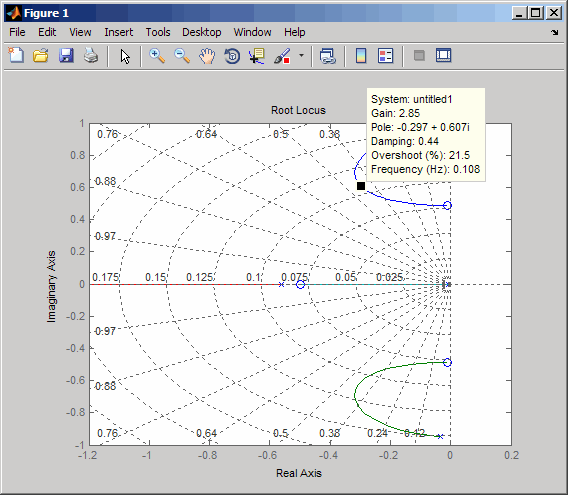
Затем, закройте обратную связь SISO.
K = 2.85;
cl11 = feedback(sys11,-K); % Note: feedback assumes negative
% feedback by default
Постройте импульсный ответ с обратной связью на срок 20 секунд и сравните его с импульсным ответом разомкнутого цикла.
impulse(sys11,'b--',cl11,'r',20)
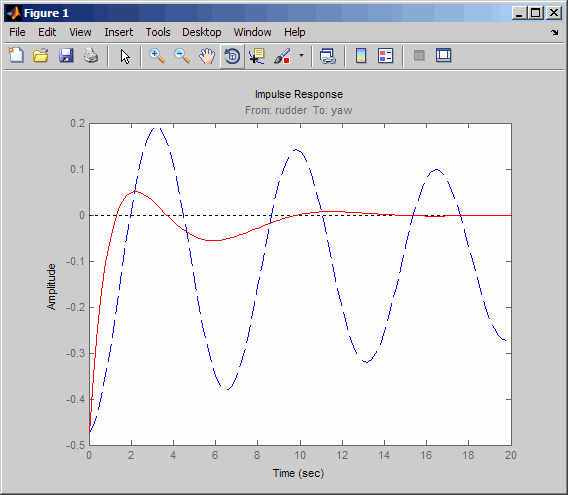
Ответ с обратной связью обосновывается быстро и не колеблется очень, особенно когда по сравнению с ответом разомкнутого цикла.
Теперь замкните круг на полной модели MIMO и смотрите, как ответ от элерона смотрит. Обратная связь включает вход 1 и вывела 1 из объекта (используйте feedback с индексными векторами, выбирающими эту пару ввода/вывода). В подсказке MATLAB® ввести
cloop = feedback(sys,-K,1,1);
damp(cloop) % closed-loop poles
Pole Damping Frequency Time Constant
(rad/seconds) (seconds)
-3.42e-01 1.00e+00 3.42e-01 2.92e+00
-2.97e-01 + 6.06e-01i 4.40e-01 6.75e-01 3.36e+00
-2.97e-01 - 6.06e-01i 4.40e-01 6.75e-01 3.36e+00
-1.05e+00 1.00e+00 1.05e+00 9.50e-01 Постройте импульсный ответ MIMO.
impulse(sys,'b--',cloop,'r',20)
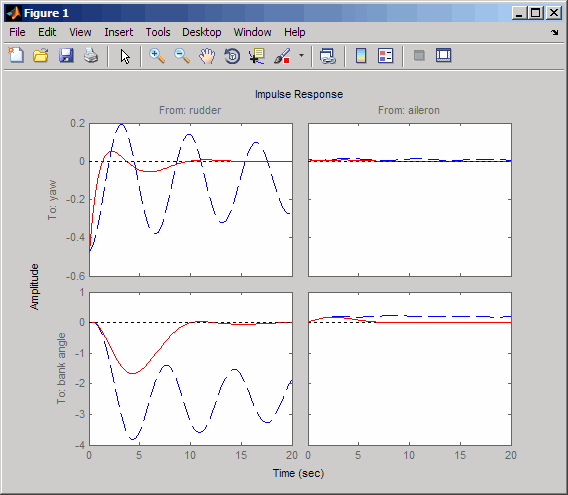
Ответ уровня отклонения от курса теперь хорошо ослабляется, но посмотрите на график от элерона (введите 2) к углу банка (выводит 2). Когда вы перемещаете элерон, система больше не продолжает управлять банком как нормальный самолет. Вы сверхстабилизировали спиральный режим. Спиральный режим обычно является очень медленным режимом и позволяет самолету управлять банком и поворачиваться без постоянного входа элерона. Пилоты используются к этому поведению и не будут любить ваш проект, если это не позволяет им обычно лететь. Этот проект переместил спиральный режим так, чтобы это имело более быструю частоту.
То, что необходимо сделать, убеждаются, что спиральный режим не перемещается далее в левую полуплоскость, когда вы замыкаете круг. Одним путем разработчики управления полетом решили эту проблему, должен использовать фильтр размытия kH (s) где
Фильтр размытия помещает нуль в начале координат, которое ограничивает спиральный полюс режима оставаться около источника. Мы выбираем α = 0.2 какое-то время постоянный из пяти секунд и используем метод корневого годографа, чтобы выбрать усиление фильтра H. Сначала задайте фиксированную часть s / (s + α) размытия
H = zpk(0,-0.2,1);
Соедините размытие последовательно с моделью проекта sys11 (отношение между входом 1 и выведите 1) получить модель разомкнутого цикла
oloop = H * sys11;
и чертите другой корневой годограф для этой модели разомкнутого цикла.
rlocus(-oloop) sgrid
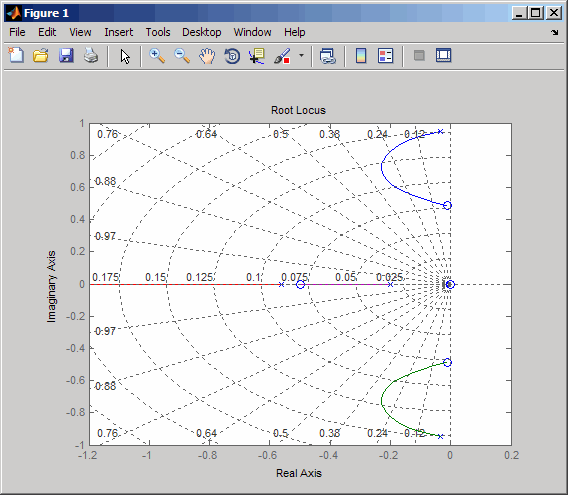
Создайте и перетащите маркер данных вокруг верхней кривой, чтобы определить местоположение максимального затухания, которое является о ζ = 0.3.
Эти данные показывают маркер данных в максимальном отношении затухания; усиление - приблизительно 2,07.
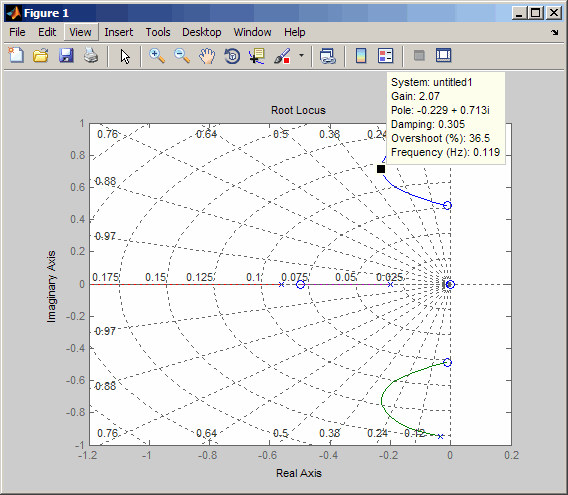
Посмотрите на ответ с обратной связью от руководящего принципа, чтобы отклоняться от курса уровень.
K = 2.07; cl11 = feedback(oloop,-K); impulse(cl11,20)
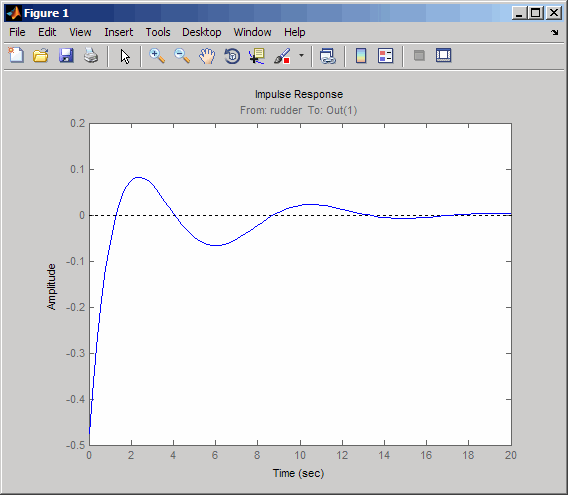
Ответ обосновывается приятно, но имеет меньше затухания, чем ваш предыдущий проект. Наконец, можно проверить, что фильтр размытия решил спиральную проблему режима. Сначала сформируйтесь, полное размытие фильтруют kH (s) (размытие + усиление).
WOF = -K * H;
Затем замкните круг вокруг первой пары ввода-вывода модели MIMO sys и моделируйте импульсный ответ.
cloop = feedback(sys,WOF,1,1); % Final closed-loop impulse response impulse(sys,'b--',cloop,'r',20)
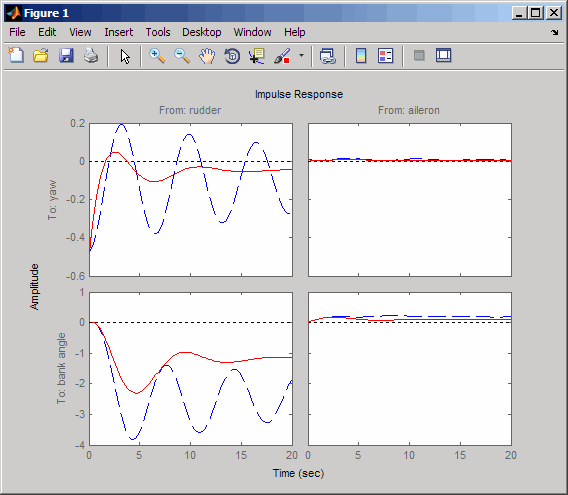
Угловой ответ банка (выводит 2) из-за импульса элерона (вводит 2) теперь имеет желаемое почти постоянное поведение по этому кратковременному кадру. Чтобы осмотреть ответ более тесно, используйте Селектор ввода-вывода в контекстном меню, чтобы выбрать (2,2) пара ввода-вывода.
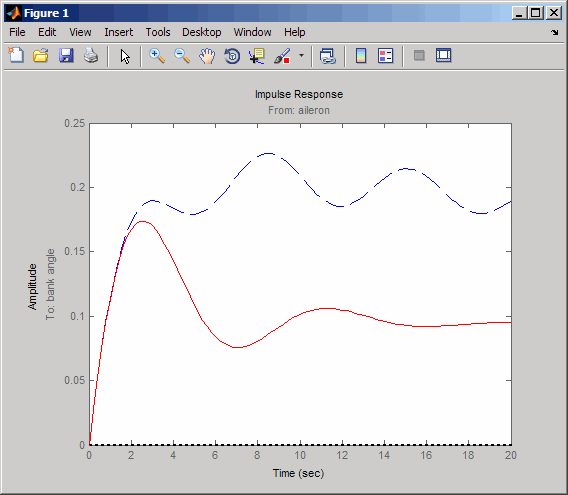
Несмотря на то, что вы действительно не совсем соответствовали спецификации затухания, ваш проект увеличил затухание системы существенно и теперь позволяет пилоту обычно управлять самолетом.