Документация

Ряд времени проектирования нейронные сети обратной связи NARX

Чтобы видеть примеры использования сетей NARX, применяемых в форме разомкнутого цикла, форме с обратной связью и открытом / замкнутом цикле многоступенчатый прогноз, см. Многоступенчатый Прогноз Нейронной сети.

Все определенные динамические сети, обсужденные до сих пор, или были фокусируемыми сетями с динамикой только на входном слое или feedforward сетях. Нелинейная авторегрессивная сеть с внешними входными параметрами (NARX) является текущей динамической сетью со связями обратной связи, заключающими несколько слоев сети. Модель NARX основана на линейной модели ARX, которая обычно используется в моделировании timeseries.

Уравнение определения для модели NARX

где следующее значение зависимого выходного сигнала y (t) регрессируется на предыдущих значениях выходного сигнала и предыдущих значениях независимого (внешнего) входного сигнала. Можно реализовать модель NARX при помощи feedforward нейронной сети, чтобы аппроксимировать функциональный f. Схему получившейся сети показывают ниже, где 2D слой feedforward сеть используется для приближения. Эта реализация также допускает векторную модель ARX, где ввод и вывод может быть многомерным.

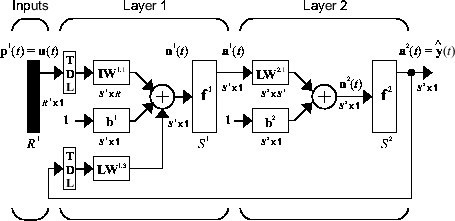
Существует много приложений для сети NARX. Это может использоваться в качестве предиктора, чтобы предсказать следующее значение входного сигнала. Это может также использоваться для нелинейной фильтрации, в которой целевой вывод является бесшумной версией входного сигнала. Использование сети NARX показывают в другом важном приложении, моделировании нелинейных динамических систем.

Прежде, чем показать обучение сети NARX, важная настройка, которая полезна в учебном объяснении потребностей. Можно полагать, что вывод сети NARX оценка вывода некоторой нелинейной динамической системы, что вы пытаетесь смоделировать. Вывод возвращен к входу feedforward нейронной сети как часть стандартной архитектуры NARX, как показано в покинутой фигуре ниже. Поскольку истинный вывод доступен во время обучения сети, вы могли создать последовательно-параллельную архитектуру (см. [NaPa91]), в котором истинный вывод используется вместо того, чтобы возвратить предполагаемый вывод, как показано в правильной фигуре ниже. Это имеет два преимущества. Прежде всего, вход к feedforward сети более точен. Второе - то, что получившаяся сеть имеет просто feedforward архитектура, и статическая обратная связь может использоваться для обучения.

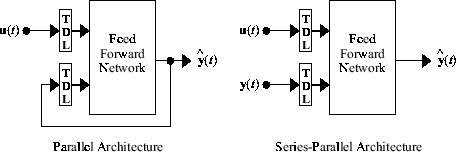
Следующее показывает использование последовательно-параллельной архитектуры для того, чтобы обучить сеть NARX, чтобы смоделировать динамическую систему.

Примером сети NARX является система магнитной левитации, описал начало в Использовании диспетчер NARMA-L2 Блок. Нижний график в следующей фигуре показывает, что напряжение применилось к электромагниту, и главный график показывает положение постоянного магнита. Данные были собраны в интервале выборки 0,01 секунд, чтобы сформировать два временных рядов.

Цель состоит в том, чтобы разработать модель NARX для этой системы магнитной левитации.

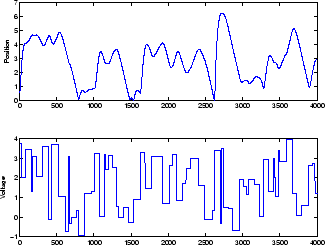
Во-первых, загрузите данные тренировки. Используйте коснувшиеся строки задержки с двумя задержками и входа и вывода, таким образом обучение начинается с третьей точки данных. Существует два входных параметров к последовательно-параллельной сети, u (t) последовательность и y (t) последовательность.

load magdata
y = con2seq(y);
u = con2seq(u);

Создайте последовательно-параллельную сеть NARX с помощью функционального narxnet. Используйте 10 нейронов в скрытом слое и используйте trainlm для учебной функции, и затем подготовьте данные с preparets:

d1 = [1:2];
d2 = [1:2];
narx_net = narxnet(d1,d2,10);
narx_net.divideFcn = '';
narx_net.trainParam.min_grad = 1e-10;
[p,Pi,Ai,t] = preparets(narx_net,u,{},y);

(Заметьте, что последовательность y рассматривается сигналом обратной связи, который является входом, который является также выводом (цель). Позже, когда вы замыкаете круг, соответствующий вывод будет соединен с соответствующим входом.) Теперь вы готовы обучить сеть.

narx_net = train(narx_net,p,t,Pi);

Можно теперь моделировать сеть и построить получившиеся ошибки для последовательно-параллельной реализации.

yp = sim(narx_net,p,Pi);
e = cell2mat(yp)-cell2mat(t);
plot(e)

Вы видите, что ошибки являются очень небольшими. Однако из-за последовательно-параллельной настройки, это ошибки только для прогноза "один шаг вперед". Более строгий тест должен был бы перестроить сеть в исходную параллельную форму (замкнутый цикл) и затем выполнять выполненный с помощью итераций прогноз по многим временным шагам. Теперь параллельную операцию показывают.

Существует функция тулбокса (closeloop) для преобразования NARX (и другой) сети от последовательно-параллельной настройки (разомкнутый цикл), который полезен для обучения к параллельной настройке (замкнутый цикл), который полезен для многоступенчатого вперед прогноза. Следующая команда иллюстрирует, как преобразовать сеть, которую вы только обучили, чтобы быть параллельными форме:

narx_net_closed = closeloop(narx_net);

Чтобы видеть различия между этими двумя сетями, можно использовать команду представления:

view(narx_net)

view(narx_net_closed)

Все обучение сделано в разомкнутом цикле (также названный последовательно-параллельной архитектурой), включая валидацию и тестирующие шаги. Типичный рабочий процесс должен полностью создать сеть в разомкнутом цикле, и только когда это было обучено (который включает валидацию, и тестирующие шаги) преобразованный к замкнутому циклу для многоступенчатого вперед прогноза. Аналогично, значения R в графический интерфейсе пользователя вычисляются на основе результатов обучения разомкнутого цикла.

Можно теперь использовать (параллельную) настройку с обратной связью, чтобы выполнить выполненный с помощью итераций прогноз 900 временных шагов. В этой сети необходимо загрузить два начальных входных параметров и два начальных выходных параметров как начальные условия. Можно использовать функцию preparets, чтобы подготовить данные. Это будет использовать сетевую структуру, чтобы определить, как разделить и переключить данные соответственно.

y1 = y(1700:2600);
u1 = u(1700:2600);
[p1,Pi1,Ai1,t1] = preparets(narx_net_closed,u1,{},y1);
yp1 = narx_net_closed(p1,Pi1,Ai1);
TS = size(t1,2);
plot(1:TS,cell2mat(t1),'b',1:TS,cell2mat(yp1),'r')

Фигура иллюстрирует выполненный с помощью итераций прогноз. Синяя строка является фактическим положением магнита, и красная линия является положением, предсказанным нейронной сетью NARX. Даже при том, что сеть предсказывает 900 временных шагов вперед, прогноз очень точен.

Для параллельного ответа (выполненный с помощью итераций прогноз), чтобы быть точным, важно, чтобы сеть была обучена так, чтобы ошибки в последовательно-параллельной настройке (прогноз "один шаг вперед") были очень небольшими.

Можно также создать параллель (замкнутый цикл) сеть NARX, с помощью команды narxnet с четвертым набором входного параметра к 'closed', и обучить ту сеть непосредственно. Обычно обучение занимает больше времени, и получившаяся производительность не так хороша, как это получило с последовательно-параллельным обучением.

Каждый раз нейронная сеть обучена, может привести к различному решению из-за различного начального веса и сместить значения и различные деления данных в обучение, валидацию и наборы тестов. В результате различные нейронные сети, обученные на той же проблеме, могут дать различные выходные параметры для того же входа. Чтобы гарантировать, что нейронная сеть хорошей точности была найдена, переобучайтесь несколько раз.

Существует несколько других методов для того, чтобы улучшить начальные решения, если более высокая точность желаема. Для получения дополнительной информации смотрите, Улучшают Мелкое Обобщение Нейронной сети и Стараются не Сверхсоответствовать.

[X,T] = ph_dataset;

net = narxnet(10);
[x,xi,ai,t] = preparets(net,X,{},T);
net = train(net,x,t,xi,ai);
y = net(x,xi,ai);
e = gsubtract(t,y);