Вот радиальная базисная сеть с входными параметрами R.
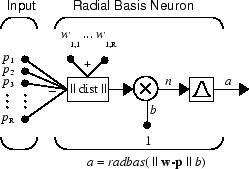
Заметьте, что выражение для сетевого входа нейрона radbas отличается от того из других нейронов. Здесь сетевой вход к передаточной функции radbas является векторным расстоянием между своим вектором веса w и входным вектором p, умноженный на смещение b. (|| dist || окружает эту фигуру, принимает входной вектор p и входную матрицу веса одной строки, и производит скалярное произведение двух.)
Передаточная функция для радиального базисного нейрона
Вот график передаточной функции radbas.
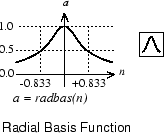
Радиальная основная функция имеет максимум 1, когда его вход 0. Как расстояние между w и уменьшениями p, выходными увеличениями. Таким образом радиальный базисный нейрон действует как детектор, который производит 1 каждый раз, когда вход p идентичен своему вектору веса w.
Смещение b позволяет чувствительности нейрона radbas быть настроенной. Например, если бы нейрон имел смещение 0,1, то он вывел бы 0.5 для любого входного вектора p на векторном расстоянии 8,326 (0.8326/b) от его вектора веса w.
Радиальные базисные сети состоят из двух слоев: скрытый радиальный базисный слой S 1 нейрон и вывод линейный слой S 2 нейрона.
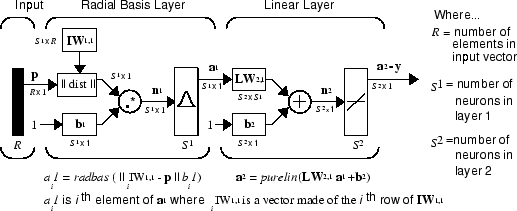
|| dist || окружает эту фигуру, принимает входной вектор p и входную матрицу IW1,1 веса, и производит вектор, имеющий S 1 элемент. Элементы являются расстояниями между входным вектором и векторами i IW1,1, сформированными из строк входной матрицы веса.
Вектор смещения b1 и вывод || dist, || объединен с операцией MATLAB®.*, который делает поэлементно умножение.
Вывод первого слоя для feedforward сети net может быть получен со следующим кодом:
a{1} = radbas(netprod(dist(net.IW{1,1},p),net.b{1}))
К счастью, вы не должны будете писать такие строки кода. Все подробности разработки этой сети встроены в функции проекта newrbe и newrb, и можно получить их выходные параметры с sim.
Можно понять, как эта сеть ведет себя следующим входной вектор p через сеть к выводу a2. Если вы представите входной вектор такой сети, каждый нейрон в радиальном базисном слое выведет значение согласно тому, как близко входной вектор к вектору веса каждого нейрона.
Таким образом радиальные базисные нейроны с векторами веса, очень отличающимися от входного вектора p, имеют выходные параметры около нуля. Эти маленькие выходные параметры имеют только незначительный эффект на линейные выходные нейроны.
Напротив, радиальный базисный нейрон с вектором веса близко к входному вектору p производит значение около 1. Если нейрон имеет вывод 1, его выходные веса во втором слое передают свои значения линейным нейронам во втором слое.
На самом деле, если бы только один радиальный базисный нейрон имел вывод 1, и у всех других были выходные параметры 0s (или очень близко к 0), вывод линейного слоя был бы выходными весами активного нейрона. Это, однако, было бы крайним случаем. Обычно несколько нейронов всегда стреляют в различных степенях.
Теперь посмотрите подробно на то, как первый слой действует. Взвешенный вход каждого нейрона является расстоянием между входным вектором и его вектором веса, вычисленным с dist. Сетевой вход каждого нейрона поэлементно продукт его взвешенного входа с его смещением, вычисленным с netprod. Вывод каждого нейрона является своим сетевым входом, прошел через radbas. Если вектор веса нейрона равен (транспонированному) входному вектору, его взвешенный вход 0, его сетевой вход 0, и его вывод равняется 1. Если вектор веса нейрона является расстоянием spread от входного вектора, его взвешенным входом является spread, его сетевой вход является sqrt (−log (.5)) (или 0.8326), поэтому его вывод 0.5.
Можно разработать радиальные базисные сети с функциональным newrbe. Эта функция может произвести сеть с нулевой ошибкой на учебных векторах. Это называется следующим образом:
net = newrbe(P,T,SPREAD)
Функциональный newrbe берет матрицы входных векторов P и целевые векторы T и распространение постоянный SPREAD для радиального базисного слоя, и возвращает сеть с весами и смещает таким образом, что выходными параметрами является точно T, когда входными параметрами является P.
Этот функциональный newrbe создает столько же нейронов radbas, сколько существуют входные векторы в P, и устанавливает веса первого слоя на P'. Таким образом существует слой нейронов radbas, в которых каждый нейрон действует как детектор для различного входного вектора. Если будут входные векторы Q, то будут нейроны Q.
Каждое смещение в первом слое установлено в 0.8326/SPREAD. Это дает радиальные основные функции, которые пересекаются 0.5 во взвешенных входных параметрах +/− SPREAD. Это определяет ширину области на входном пробеле, на который отвечает каждый нейрон. Если SPREAD будет равняться 4, то каждый нейрон radbas ответит 0.5 или больше к любым входным векторам на векторном расстоянии 4 от их вектора веса. SPREAD должен быть достаточно большим, что нейроны строго отвечают на перекрывающиеся области входного пробела.
Веса IW 2,1 второго слоя (или в коде, IW{2,1}) и смещения b2 (или в коде, b{2}) найдены путем симуляции первого слоя выходные параметры a1 (A{1}), и затем решения следующего линейного выражения:
[W{2,1} b{2}] * [A{1}; ones(1,Q)] = T
Вы знаете входные параметры к второму слою (A{1}) и цель (T), и слой линеен. Можно использовать следующий код, чтобы вычислить веса и смещения второго слоя, чтобы минимизировать квадратичную невязку суммы.
Wb = T/[A{1}; ones(1,Q)]
Здесь Wb содержит и веса и смещения со смещениями в последнем столбце. Квадратичная невязка суммы всегда 0, как объяснено ниже.
Существует проблема с ограничениями C (пары входа/цели), и каждый нейрон имеет C +1 переменная (веса C от нейронов radbas C и смещение). Линейная задача с ограничениями C и больше, чем переменные C имеет бесконечное число нулевых ошибочных решений.
Таким образом newrbe создает сеть с нулевой ошибкой на учебных векторах. Единственное требуемое условие состоит в том, чтобы убедиться, что SPREAD является достаточно большим, который активные входные области нейронов radbas перекрывают достаточно так, чтобы несколько нейронов radbas всегда имели довольно крупносерийные производства в любой данный момент. Это делает сетевую функцию более сглаженной и приводит к лучшему обобщению для новых входных векторов, происходящих между входными векторами, используемыми в проекте. (Однако SPREAD не должен быть столь большим, что каждый нейрон эффективно отвечает в той же большой площади входного пробела.)
Недостаток к newrbe - то, что он производит сеть со столькими же скрытых нейронов, сколько существуют входные векторы. Поэтому newrbe не возвращает приемлемое решение, когда много входных векторов необходимы, чтобы правильно задать сеть, когда обычно имеет место.
Функциональный newrb итеративно создает радиальное основание, объединяют один нейрон в сеть за один раз. Нейроны добавляются к сети до падений квадратичной невязки суммы ниже ошибочной цели, или максимальное количество нейронов было достигнуто. Призыв к этой функции
net = newrb(P,T,GOAL,SPREAD)
Функциональный newrb берет матрицы входа и целевых векторов P и T и параметры проекта GOAL и SPREAD, и возвращает желаемую сеть.
Метод разработки newrb подобен тому из newrbe. Различие - то, что newrb создает нейроны по одному. В каждой итерации входной вектор, который приводит к понижению сетевой ошибки большинство, используется, чтобы создать нейрон radbas. Ошибка новой сети проверяется, и, если низкий достаточно newrb закончено. В противном случае следующий нейрон добавляется. Эта процедура повторяется, пока ошибочной цели не удовлетворяют, или максимальное количество нейронов достигнуто.
Как с newrbe, важно, чтобы параметр распространения был достаточно большим, что нейроны radbas отвечают на перекрывающиеся области входного пробела, но не столь большие, что все нейроны отвечают по существу тем же способом.
Почему не всегда используют радиальную базисную сеть вместо стандарта feedforward сеть? Радиальные базисные сети, даже когда разработано эффективно с newrbe, имеют тенденцию иметь много раз больше нейронов, чем сопоставимая feedforward сеть с tansig или нейронов logsig в скрытом слое.
Это вызвано тем, что сигмоидальные нейроны могут иметь выходные параметры по большой области входного пробела, в то время как нейроны radbas только отвечают на относительно небольшие области входного пробела. Результат состоит в том, что, чем больше входной пробел (с точки зрения количества входных параметров и областей значений те входные параметры отличаются), тем больше нейронов radbas потребовало.
С другой стороны, разработка радиальной базисной сети часто занимает намного меньше времени, чем обучение сигмоидальной/линейной сети и может иногда приводить к тому, что меньше нейроны были используемыми, как видно в следующем примере.
demorb1 в качестве примера показывает, как радиальная базисная сеть используется, чтобы соответствовать функции. Здесь проблема решена только с пятью нейронами.
Примеры demorb3 и demorb4 исследуют как распространение постоянное влияние процесс проектирования для радиальных базисных сетей.
В demorb3 радиальная базисная сеть разработана, чтобы решить ту же проблему как в demorb1. Однако на этот раз распространение, постоянное используемый, 0.01. Таким образом каждый радиальный базисный нейрон возвращается 0.5 или ниже для любого входного вектора с расстоянием 0.01 или больше от его вектора веса.
Поскольку учебные входные параметры происходят с промежутками в 0,1, никакие два радиальных базисных нейрона не имеют сильный вывод ни для какого данного входа.
demorb3 показал, что наличие слишком маленького постоянного распространения может привести к решению, которое не делает вывод из векторов входа/цели, используемых в проекте. Пример demorb4 показывает противоположную проблему. Если постоянное распространение будет достаточно большим, радиальные базисные нейроны выведут большие значения (около 1.0) для всех входных параметров, используемых, чтобы разработать сеть.
Если все радиальные базисные нейроны всегда выводят 1, любая информация, представленная сети, становится потерянной. Неважно, что вход, второй слой выходные параметры 1. Функциональный newrb попытается найти сеть, но не может из-за числовых проблем, которые возникают в этой ситуации.
Мораль истории, выберите распространение, постоянное больше, чем расстояние между смежными входными векторами, чтобы получить хорошее обобщение, но меньший, чем расстояние через целый входной пробел.
Для этой проблемы, которая означала бы выбирать распространение, постоянное больше, чем 0,1, интервал между входными параметрами, и меньше чем 2, расстоянием между крайними левыми и самыми правыми входными параметрами.