Этот раздел обеспечивает пример того, как можно создать фильтр с целочисленными коэффициентами. В этом примере создается фильтр повышенного косинуса с коэффициентами с плавающей точкой, и коэффициенты фильтра затем преобразованы в целые числа.
Чтобы проиллюстрировать концепции использования целых чисел с фильтрами фиксированной точки, этот пример будет использовать фильтр повышенного косинуса:
b = rcosdesign(.25, 12.5, 8, 'sqrt');
b нормированы так, чтобы усиление полосы пропускания было равным 1 и было все меньшим, чем 1. В порядке сделать их целыми числами, они должны будут масштабироваться. Если вы хотели масштабировать их, чтобы использовать 18 битов для каждого коэффициента, область значений возможных значений для коэффициентов становится:
Поскольку самый большой коэффициент b положителен, это должно будет масштабироваться максимально близко к 131 071 (не переполняясь) в порядке минимизировать ошибку квантования. Можно определить экспоненту масштабного коэффициента путем выполнения:
B = 18; % Number of bits L = floor(log2((2^(B-1)-1)/max(b))); % Round towards zero to avoid overflow bsc = b*2^L;
Также можно использовать инструмент автомасштабирования чисел фиксированной точки можно следующим образом:
bq = fi(b, true, B); % signed = true, B = 18 bits L = bq.FractionLength;
Это - совпадение, что B и L оба 18 в этом случае из-за значения самого большого коэффициента b. Если бы, например, максимальное значение b было 0.124, L был бы 20, в то время как B (количество битов) останется 18.
Сначала создайте фильтр с помощью прямой формы, коснувшейся структуры строки задержки:
h = dfilt.dffir(bsc);
В порядке установить обязательные параметры, арифметика должна быть установлена в фиксированную точку:
h.Arithmetic = 'fixed'; h.CoeffWordLength = 18;
Можно проверять, что коэффициенты h являются всеми целыми числами:
all(h.Numerator == round(h.Numerator)) ans = 1
Теперь можно исследовать ответ значения фильтра с помощью fvtool:
fvtool(h, 'Color', 'white')
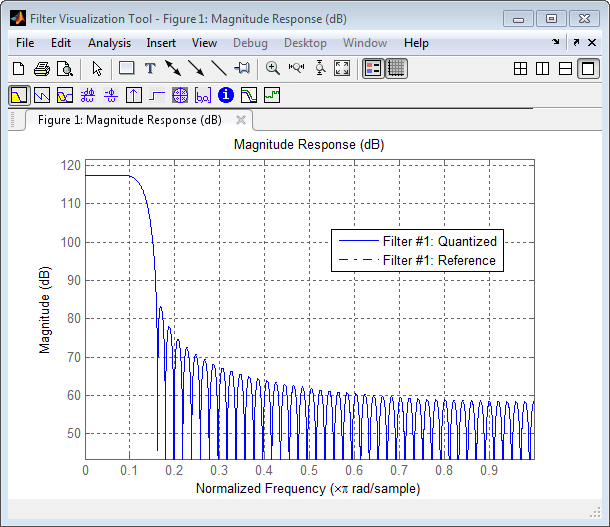
Это показывает большое усиление 117 дБ в полосе пропускания, которая происходит из-за больших значений коэффициентов — это заставит вывод фильтра быть намного больше, чем вход. Метод обращения к этому будет обсужден в следующих разделах.
Необходимо будет установить входные параметры фильтра к соответствующим значениям для работы с целыми числами. Например, если вход к фильтру от конвертера A/D с 12 битовыми разрешениями, необходимо установить вход можно следующим образом:
h.InputWordLength = 12; h.InputFracLength = 0;
Метод info возвращает сводные данные настроек фильтра.
info(h)
Discrete-Time FIR Filter (real) ------------------------------- Filter Structure : Direct-Form FIR Filter Length : 101 Stable : Yes Linear Phase : Yes (Type 1) Arithmetic : fixed Numerator : s18,0 -> [-131072 131072) Input : s12,0 -> [-2048 2048) Filter Internals : Full Precision Output : s31,0 -> [-1073741824 1073741824) (auto determined) Product : s29,0 -> [-268435456 268435456) (auto determined) Accumulator : s31,0 -> [-1073741824 1073741824) (auto determined) Round Mode : No rounding Overflow Mode : No overflow
В этом случае все дробные длины теперь обнуляются, означая, что фильтр h настраивается, чтобы обработать целые числа.
Можно сгенерировать входной сигнал для фильтра путем квантования к 12 битам, использующим автомасштабирующуюся функцию, или можно выполнить ту же процедуру, которая использовалась для коэффициентов, обсудил ранее. В этом примере создайте сигнал с двумя синусоидами:
n = 0:999; f1 = 0.1*pi; % Normalized frequency of first sinusoid f2 = 0.8*pi; % Normalized frequency of second sinusoid x = 0.9*sin(0.1*pi*n) + 0.9*sin(0.8*pi*n); xq = fi(x, true, 12); % signed = true, B = 12 xsc = fi(xq.int, true, 12, 0);
Чтобы отфильтровать входной сигнал, сгенерированный выше, введите следующее:
ysc = filter(h, xsc);
Здесь ysc является полной точностью вывод, означая, что никакие биты не были отброшены в вычислении. Это делает ysc самым лучшим выводом, которого можно достигнуть, учитывая 12-битный вход и 18-битные коэффициенты. Это может быть проверено путем фильтрации использования с двойной точностью с плавающей точкой и сравнение результатов двух операций фильтрации:
hd = double(h);
xd = double(xsc);
yd = filter(hd, xd);
norm(yd-double(ysc))
ans =
0
Теперь можно исследовать вывод по сравнению с входом. Этот пример строит только последние несколько выборок, чтобы минимизировать эффект переходных процессов:
idx = 800:950;
xscext = double(xsc(idx)');
gd = grpdelay(h, [f1 f2]);
yidx = idx + gd(1);
yscext = double(ysc(yidx)');
stem(n(idx)', [xscext, yscext]);
axis([800 950 -2.5e8 2.5e8]);
legend('input', 'output');
set(gcf, 'color', 'white');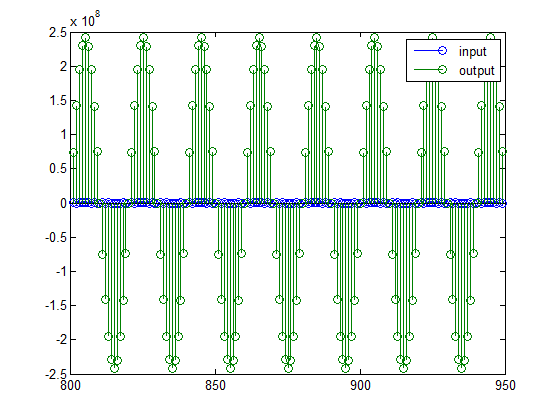
Трудно сравнить два сигнала в этой фигуре из-за значительных различий в шкалах. Это происходит из-за большого усиления фильтра, таким образом, необходимо будет компенсировать усиление фильтра:
stem(n(idx)', [2^18*xscext, yscext]);
axis([800 950 -5e8 5e8]);
legend('scaled input', 'output');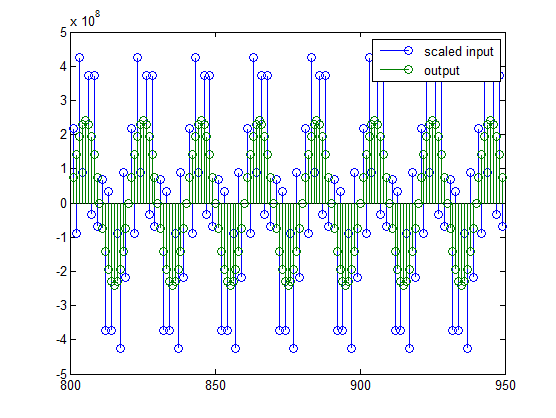
Вы видите, как сигналы выдерживают сравнение намного более легко, если масштабирование было сделано, как замечено в вышеупомянутой фигуре.
Если вы исследуете вывод wordlength,
ysc.WordLength
ans =
31
вы заметите, что количество битов в выводе значительно больше, чем во входе. Поскольку такой рост в количестве битов, представляющих данные, не может быть желательным, вы, возможно, должны обрезать wordlength вывода. Лучший способ сделать это должно отбросить младшие значащие биты в порядке минимизировать ошибку. Однако, если вы знаете, что существуют неиспользованные высокого уровня биты, необходимо отбросить те биты также.
Чтобы определить, существуют ли неиспользованные старшие значащие биты (MSBs), можно посмотреть на то, где рост в WordLength возникает в вычислении. В этом случае рост разрядности происходит, чтобы разместить результаты добавляющих продуктов входа (12 битов) и коэффициентов (18 битов). Каждый из этих продуктов 29 битов длиной (можно проверить это использование info(h)). Рост разрядности из-за накопления продукта зависит от длины фильтра и содействующих значений - однако, это - определение худшего случая в том смысле, что никакое предположение на входном сигнале не сделано кроме того, и в результате может быть неиспользованный MSBs. Необходимо будет быть осторожными, хотя, когда MSBs, которые считают неиспользованными неправильно, вызовут переполнение.
Предположим, что вы хотите сохранить 16 битов для вывода. В этом случае нет никакого роста разрядности из-за сложений, таким образом, выходная установка бита будет 16 для wordlength и –14 для дробной длины.
Поскольку фильтрация была уже сделана, можно отбросить некоторые биты от ysc:
yout = fi(ysc, true, 16, -14);
Также можно установить фильтр выходные длины бита непосредственно (это полезно, если вы планируете фильтрацию многих сигналов):
specifyall(h); h.OutputWordLength = 16; h.OutputFracLength = -14; yout2 = filter(h, xsc);
Можно проверить, что результатами является то же самое так или иначе:
norm(double(yout) - double(yout2))
ans =
0
Однако, если вы сравните это с полной точностью вывод, вы заметите, что существует погрешность округления из-за отброшенных битов:
norm(double(yout)-double(ysc))
ans =
1.446323386867543e+005
В этом случае различия трудно определить при отображении данных на графике, как замечено ниже:
stem(n(yidx), [double(yout(yidx)'), double(ysc(yidx)')]);
axis([850 950 -2.5e8 2.5e8]);
legend('Scaled Input', 'Output');
set(gcf, 'color', 'white');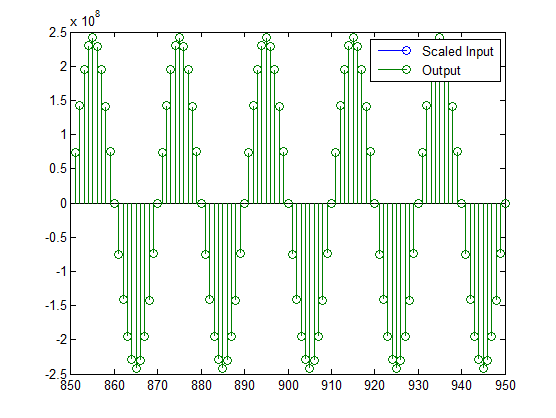
Поскольку фильтр в этом примере имеет такое большое усиление, вывод в различной шкале, чем вход. Это масштабирование является чисто теоретическим однако, и можно масштабировать данные однако, вам нравится. В этом случае у вас есть 16 битов для вывода, но можно присоединить любое масштабирование, вы выбираете. Было бы естественно дать иное толкование выводу, чтобы иметь вес 2^0 (или L = 0) для LSB. Это эквивалентно уменьшению масштаба выходного сигнала фактором 2^ (-14). Однако нет никакого вычисления или включенной погрешности округления. Можно сделать это путем выполнения следующего:
yri = fi(yout.int, true, 16, 0);
stem(n(idx)', [xscext, double(yri(yidx)')]);
axis([800 950 -1.5e4 1.5e4]);
legend('input', 'rescaled output');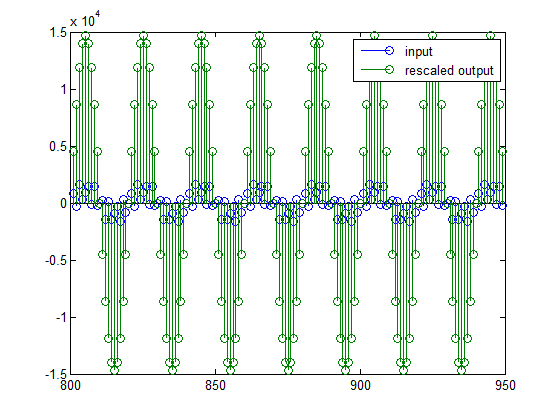
Этот график показывает, что вывод еще больше, чем вход. Если бы вы сделали просачивание с двойной точностью с плавающей точкой, это не имело бы место — потому что здесь больше битов используется для вывода, чем для входа, таким образом, MSBs взвешиваются по-другому. Вы видите это иначе путем рассмотрения ответа значения масштабированного фильтра:
[H,w] = freqz(h); plot(w/pi, 20*log10(2^(-14)*abs(H)));
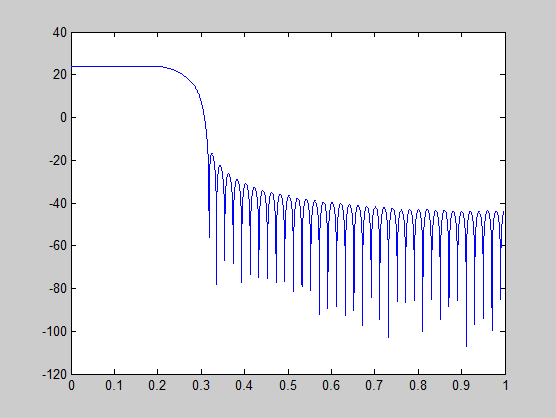
Этот график показывает, что усиление полосы пропускания все еще выше 0 дБ.
Чтобы поместить ввод и вывод на ту же шкалу, MSBs должен быть взвешен одинаково. Вход MSB имеет вес 2^11, тогда как масштабированный вывод MSB имеет вес 2^ (29–14) = 2^15. Необходимо дать выводу MSB вес 2^11 можно следующим образом:
yf = fi(zeros(size(yri)), true, 16, 4);
yf.bin = yri.bin;
stem(n(idx)', [xscext, double(yf(yidx)')]);
legend('input', 'rescaled output');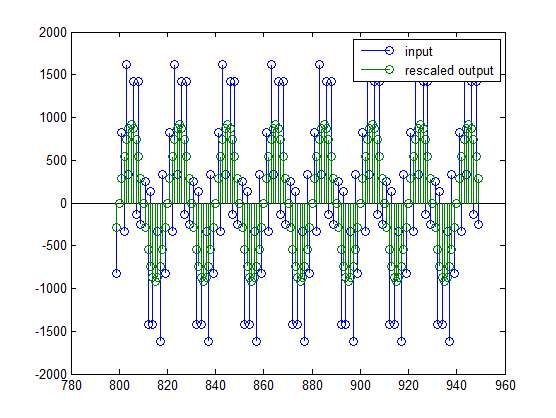
Эта операция эквивалентна уменьшению масштаба усиления фильтра 2^ (-18).
[H,w] = freqz(h); plot(w/pi, 20*log10(2^(-18)*abs(H)));
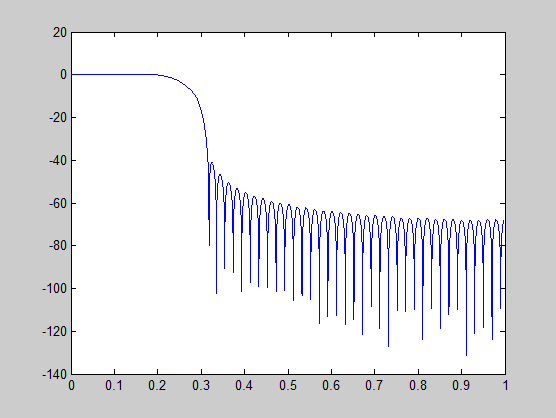
Вышеупомянутый график показывает 0 усилений дБ в полосе пропускания, как желаемый.
С этой окончательной версией вывода yf больше не является целым числом. Однако это происходит только из-за интерпретации - целые числа, представленные битами в yf, идентичны тем представленным битами в yri. Можно проверить это путем сравнения их:
max(abs(yf.int - yri.int))
ans =
0
Усадите параметры фильтра за работу с Целыми числами
Метод set2int обеспечивает удобный способ усадить параметры фильтра за работу с целыми числами. Метод работает путем масштабирования коэффициентов к целым числам и обнуления коэффициентов и ввел дробную длину. Это позволяет вам использовать коэффициенты с плавающей точкой непосредственно.
h = dfilt.dffir(b); h.Arithmetic = 'fixed';
Коэффициенты представлены с 18 битами, и входной сигнал представлен с 12 битами:
g = set2int(h, 18, 12);
g_dB = 20*log10(g)
g_dB =
1.083707984390332e+002
Метод set2int возвращает усиление фильтра путем масштабирования коэффициентов к целым числам, таким образом, усиление всегда является степенью 2. Можно проверить, что усиление, которое мы получаем здесь, сопоставимо с усилением фильтра ранее. Теперь можно также проверять, что фильтр h правильно приступается к работе с целыми числами:
info(h) Discrete-Time FIR Filter (real) ------------------------------- Filter Structure : Direct-Form FIR Filter Length : 101 Stable : Yes Linear Phase : Yes (Type 1) Arithmetic : fixed Numerator : s18,0 -> [-131072 131072) Input : s12,0 -> [-2048 2048) Filter Internals : Full Precision Output : s31,0 -> [-1073741824 1073741824) (auto determined) Product : s29,0 -> [-268435456 268435456) (auto determined) Accumulator: s31,0 -> [-1073741824 1073741824) (auto determined) Round Mode : No rounding Overflow Mode : No overflow
Здесь вы видите, что все дробные длины теперь обнуляются, таким образом, этот фильтр настраивается правильно для работы с целыми числами.
Дайте иное толкование Выводу
Можно сравнить вывод со ссылочным выводом с плавающей точкой с двойной точностью и проверить, что вычисление, сделанное фильтром h, сделано в полной точности.
yint = filter(h, xsc);
norm(yd - double(yint))
ans =
0
Можно затем обрезать вывод только до 16 битов:
yout = fi(yint, true, 16);
stem(n(yidx), [xscext, double(yout(yidx)')]);
axis([850 950 -2.5e8 2.5e8]);
legend('input', 'output');
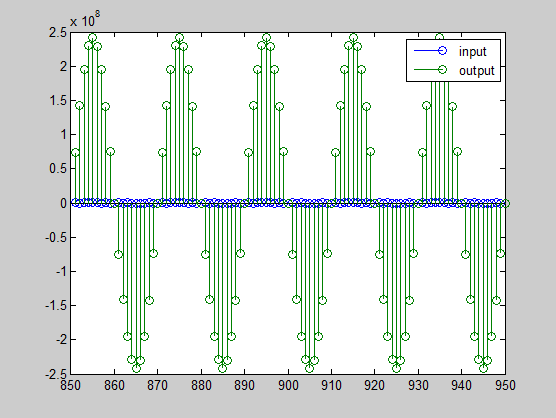
Еще раз график показывает, что ввод и вывод в различных шкалах. В порядке масштабировать вывод так, чтобы сигналы могли быть сравнены более легко в графике, необходимо будет взвесить MSBs соответственно. Можно вычислить новую дробную длину с помощью усиления фильтра, когда коэффициенты были целыми числами:
WL = yout.WordLength;
FL = yout.FractionLength + log2(g);
yf2 = fi(zeros(size(yout)), true, WL, FL);
yf2.bin = yout.bin;
stem(n(idx)', [xscext, double(yf2(yidx)')]);
axis([800 950 -2e3 2e3]);
legend('input', 'rescaled output');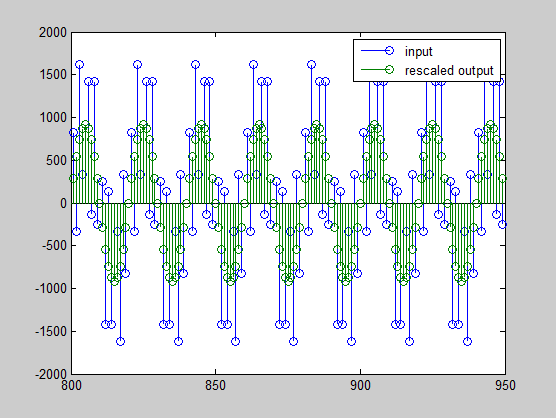
Этот итоговый график показывает отфильтрованные данные, повторно масштабируемые, чтобы совпадать с входной шкалой.