Этот пример иллюстрирует один способ использовать несколько адаптивных алгоритмов фильтра, предоставленных в тулбоксе. В этом примере приложение улучшения сигнала используется в качестве рисунка. В то время как существует приблизительно 30 различных адаптивных алгоритмов фильтрации, включенных с тулбоксом, этот пример демонстрирует два алгоритма — наименьшее количество среднего квадрата (LMS) и нормированный LMS. Оба из этих алгоритмов доступны с Системой dsp.LMSFilter object™.
Цель состоит в том, чтобы использовать адаптивный фильтр, чтобы извлечь желаемый сигнал от поврежденного шумом сигнала путем отфильтровывания шума. Желаемый сигнал (вывод от процесса) является синусоидой с 1 000 выборок.
n = (1:1000)'; s = sin(0.075*pi*n);
Выполнять адаптацию требует двух сигналов:
ссылочный сигнал
сигнал с шумом, который содержит и желаемый сигнал и добавленный шумовой компонент.
Чтобы создать шумовой сигнал, примите, что шумовой v1 авторегрессивен, означая, что значение шума во время t зависит только от своих предыдущих значений и от случайного воздействия.
v = 0.8*randn(1000,1); % Random noise part.
ar = [1,1/2]; % Autoregression coefficients.
v1 = filter(1,ar,v); % Noise signal. Applies a 1-D digital
% filter.Чтобы сгенерировать сигнал с шумом, который содержит и желаемый сигнал и шум, добавьте шумовой v1 сигнала в желаемый s сигнала. Поврежденная шумом синусоида x
x = s + v1;
где s является желаемым сигналом, и шумом является v1. Адаптивная обработка фильтра стремится восстановить s с x путем удаления v1. Завершать сигналы должно было выполнить адаптивную фильтрацию, процесс адаптации требует ссылочного сигнала.
Задайте сигнал скользящего среднего значения v2, который коррелируется с v1. Этот v2 является ссылочным сигналом для примеров.
ma = [1, -0.8, 0.4 , -0.2]; v2 = filter(ma,1,v);
Два подобных адаптивных фильтра — LMS и NLMS — формируют основание этого примера, обоих шестых порядков. Установите порядок как переменную в MATLAB® и создайте фильтры.
L = 7; lms = dsp.LMSFilter(L,'Method','LMS',... 'WeightOutputPort',true); nlms = dsp.LMSFilter(L,'Method','Normalized LMS',... 'WeightOutputPort',true);
Подобный LMS-алгоритмам имеют размер шага, который определяет объем исправления, примененного, когда фильтр адаптируется от одной итерации до следующего. Выбор соответствующего размера шага не всегда легок, обычно требуя опыта в адаптивном проекте фильтра.
Размер шага, который является слишком маленькими увеличениями время для фильтра, чтобы сходиться на наборе коэффициентов. Это становится проблемой скорости и точности.
Тот, который является слишком большим, может заставить адаптирующийся фильтр отличаться, никогда не достигая сходимости. В этом случае проблемой является устойчивость — получившийся фильтр не может быть стабильным.
Как показывает опыт, меньшие размеры шага улучшают точность сходимости фильтра, чтобы совпадать с характеристиками неизвестного, за счет времени, которое требуется, чтобы адаптироваться.
Функция maxstep объекта dsp.LMSFilter определяет максимальный размер шага, подходящий для каждого адаптивного алгоритма фильтра LMS, который все еще гарантирует, что фильтр сходится к решению. Часто, обозначение для размера шага является µ.
[mumaxlms,mumaxmselms] = maxstep(lms,x)
[mumaxnlms,mumaxmsenlms] = maxstep(nlms);
mumaxlms =
0.2096
mumaxmselms =
0.1261Первый вывод maxstep является значением, необходимым для среднего значения коэффициентов, чтобы сходиться, в то время как вторым является значение, необходимое для среднеквадратических коэффициентов, чтобы сходиться. Выбор большого размера шага часто вызывает большие изменения от значений сходимости, поэтому выбирайте меньшие размеры шага обычно.
lms.StepSize = mumaxmselms/30; nlms.StepSize = mumaxmsenlms/20;
Если вы знаете, что размер шага использует, можно установить значение размера шага, когда вы создаете объект. Например,
lms = dsp.LMSFilter(L,'Method','LMS','StepSize',0.2);
Теперь вы настроили параметры адаптивных фильтров, и вы готовы отфильтровать сигнал с шумом. Ссылочный сигнал, v2, является входом к адаптивным фильтрам. x является желаемым сигналом в этой настройке.
Посредством адаптации y, вывод фильтров, пытается эмулировать x максимально тесно.
Поскольку v2 коррелируется только с шумовым v1 компонента x, это может только действительно эмулировать v1. Сигнал ошибки (желаемый x), минус фактический вывод y, составляет оценку части x, который не коррелируется с v2 — s, сигнал извлечь от x.
[ylms,elms,wlms] = lms(v2,x); [ynlms,enlms,wnlms] = nlms(v2,x);
Для сравнения вычислите оптимального КИХ Винеровский фильтр.
bw = firwiener(L-1,v2,x); % Optimal FIR Wiener filter yw = filter(bw,1,v2); % Estimate of x using Wiener filter ew = x - yw; % Estimate of actual sinusoid
Постройте получившуюся denoised синусоиду для каждого фильтра — Винеровского фильтра, адаптивного фильтра LMS, и адаптивного фильтра NLMS — чтобы сравнить производительность различных методов.
plot(n(900:end),[ew(900:end), elms(900:end),enlms(900:end)]);
legend('Wiener filter denoised sinusoid',...
'LMS denoised sinusoid','NLMS denoised sinusoid');
xlabel('Time index (n)');
ylabel('Amplitude');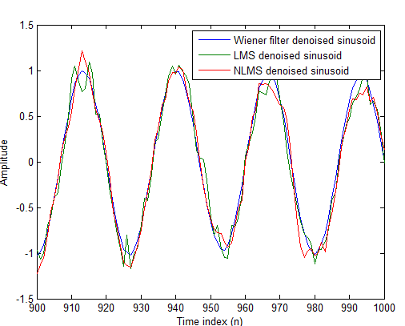
Как контрольная точка, включайте сигнал с шумом как пунктирную линию в графике.
hold on
plot(n(900:end),x(900:end),'k:')
xlabel('Time index (n)');
ylabel('Amplitude');
hold off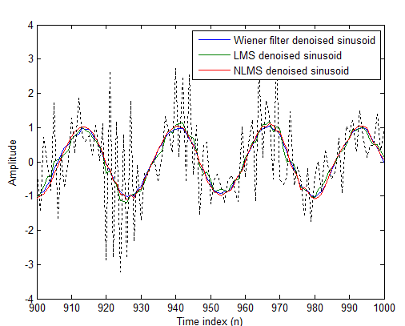
Наконец, сравните Винеровские коэффициенты фильтра с коэффициентами адаптивных фильтров. При адаптации адаптивные фильтры пытаются сходиться к Винеровским коэффициентам.
[bw.' wlms wnlms]
ans =
1.0317 0.8879 1.0712
0.3555 0.1359 0.4070
0.1500 0.0036 0.1539
0.0848 0.0023 0.0549
0.1624 0.0810 0.1098
0.1079 0.0184 0.0521
0.0492 -0.0001 0.0041Можно сбросить внутренние состояния фильтра в любое время путем вызова метода reset на объекте фильтра.
Например, следующие последовательные вызовы производят тот же вывод после сброса объекта.
[ylms,elms,wlms] = lms(v2,x); [ynlms,enlms,wnlms] = nlms(v2,x);
Если вы не сбрасываете объект фильтра, фильтр использует конечные состояния и коэффициенты от предыдущего выполнения как начальные условия для следующего запуска и набора данных.
Чтобы анализировать сходимость адаптивных фильтров, посмотрите на кривые обучения. Тулбокс предоставляет методы, чтобы сгенерировать кривые обучения, но вам нужна больше чем одна итерация эксперимента, чтобы получить значительные результаты.
Эта демонстрация использует 25 демонстрационной реализации шумных синусоид.
n = (1:5000)'; s = sin(0.075*pi*n); nr = 25; v = 0.8*randn(5000,nr); v1 = filter(1,ar,v); x = repmat(s,1,nr) + v1; v2 = filter(ma,1,v);
Теперь вычислите среднеквадратичную погрешность. Чтобы ускорить вещи, вычислите ошибку каждые 10 выборок.
Во-первых, сбросьте адаптивные фильтры, чтобы избегать использования коэффициентов, которые это уже вычислило и состояния, которые это сохранило.
reset(lms);
reset(nlms);
M = 10; % Decimation factor
mselms = msesim(lms,v2,x,M);
msenlms = msesim(nlms,v2,x,M);
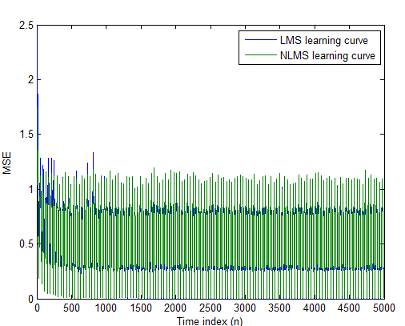
plot(1:M:n(end),[mselms,msenlms])
legend('LMS learning curve','NLMS learning curve')
xlabel('Time index (n)');
ylabel('MSE');В следующем графике вы видите расчетные кривые обучения для LMS и адаптивных фильтров NLMS.
Для LMS и алгоритмов NLMS, функции в тулбоксе помогают вам вычислить теоретические кривые обучения, наряду с минимальной среднеквадратичной погрешностью (MMSE) избыточная среднеквадратичная погрешность (EMSE) и среднее значение коэффициентов.
MATLAB может не торопиться, чтобы вычислить кривые. Фигура, показанная после кода, строит предсказанные и фактические кривые LMS.
reset(lms);
[mmselms,emselms,meanwlms,pmselms] = msepred(lms,v2,x,M);
plot(1:M:n(end),[mmselms*ones(500,1),emselms*ones(500,1),...
pmselms,mselms])
legend('MMSE','EMSE','predicted LMS learning curve',...
'LMS learning curve')
xlabel('Time index (n)');
ylabel('MSE');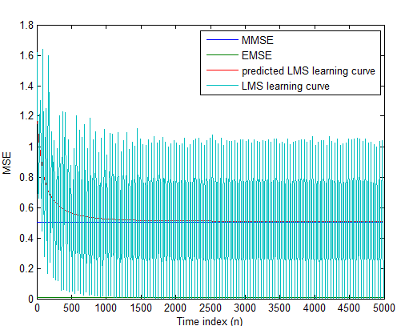
[1] Hayes, Монсон Х., статистическая цифровая обработка сигналов и Modeling, John Wiley & Sons, 1996, 493–552.
[2] Haykin, Саймон, адаптивная теория фильтра, Prentice-Hall, Inc., 1996