Блок FFT позволяет вам вывести индексы частоты в линейном или инвертированном битом порядке. Поскольку линейное упорядоченное расположение индексов частоты требует операции битного реверсирования, блок FFT может запуститься более быстро, когда выходные частоты находятся в инвертированном битом порядке.
Вход к блоку IFFT может быть в линейном или инвертированном битом порядке. Поэтому вы не должны изменять упорядоченное расположение своих данных прежде, чем преобразовать его назад во временной интервал. Однако блок IFFT может запуститься более быстро, когда вход обеспечивается в инвертированном битом порядке.
Обратите внимание на то, что БПФ и блоки ОБПФ не поддержаны в MATLAB Online.
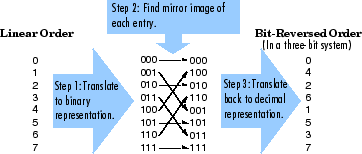
Два числа являются инвертированными битом значениями друг друга, когда бинарное представление каждый - зеркальное отображение бинарного представления другого. Например, в трехбитной системе, один и четыре инвертированные битом значения друг друга, поскольку трехбитное бинарное представление один, 001, является зеркальным отображением трехбитного бинарного представления четыре, 100. В схеме ниже, индексы частоты находятся в линейном порядке. Помещать их в инвертированный битом порядок
Переведите индексы в их бинарное представление с минимальным количеством битов. В этом примере минимальное количество битов равняется трем, потому что бинарное представление 7 равняется 111.
Найдите зеркальное отображение каждой бинарной записи и запишите его около исходного бинарного представления.
Переведите индексы назад в их десятичное представление.
Индексы частоты находятся теперь в инвертированном битом порядке.
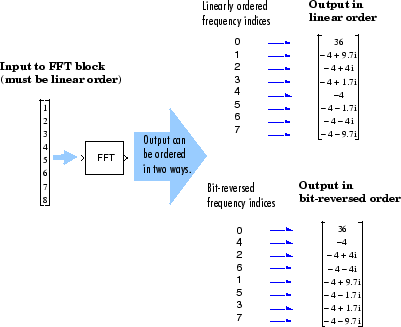
Следующая схема иллюстрирует линейные и инвертированные битом выходные параметры блока FFT. Выходные значения являются тем же самым, но они появляются в различном порядке.