Этот раздел обеспечивает вводный пример, который использует адаптивную Систему фильтра RLS object™ dsp.RLSFIlter.
Если LMS-алгоритмы представляют самое простое и наиболее легко применили адаптивные алгоритмы, алгоритмы рекурсивных наименьших квадратов (RLS) представляет увеличенную сложность, вычислительную стоимость и точность. В производительности RLS приближается к Фильтру Калмана в адаптивных приложениях фильтрации в несколько уменьшаемой необходимой пропускной способности в сигнальном процессоре.
По сравнению с LMS-алгоритмом подход RLS предлагает более быструю сходимость и меньшую ошибку относительно неизвестной системы, за счет требования большего количества вычислений.
В отличие от наименьшего количества алгоритма средних квадратичных, из которого это может быть выведено, адаптивный алгоритм RLS минимизирует общую квадратичную невязку между желаемым сигналом и выводом от неизвестной системы.
Обратите внимание на то, что пути прохождения сигнала и идентификации являются тем же самым, использует ли фильтр RLS или LMS. Различие заключается в адаптирующемся фрагменте.
В определенных рамках можно использовать любой из адаптивных алгоритмов фильтра, чтобы решить адаптивную проблему фильтра, заменяя адаптивный фрагмент приложения с новым алгоритмом.
Примеры вариантов знака LMS-алгоритмов продемонстрировали эту функцию, чтобы продемонстрировать различия между данными знака, ошибкой знака и изменениями знака знака LMS-алгоритма.
Одна интересная входная опция, которая применяется к алгоритмам RLS, не присутствует в процессах LMS — фактор упущения, λ, который определяет, как алгоритм обрабатывает прошлый ввод данных к алгоритму.
Когда LMS-алгоритм смотрит на ошибку минимизировать, это рассматривает только текущее ошибочное значение. В методе RLS рассмотренная ошибка является полной погрешностью с начала к текущей точке данных.
Сказанный иначе, алгоритм RLS имеет бесконечную память — всем ошибочным данным уделяют то же внимание в полной погрешности. В случаях, куда ошибочное значение может прибыть из побочной точки входных данных или точек, фактор упущения позволяет алгоритму RLS уменьшать значение более старых ошибочных данных путем умножения старых данных на фактор упущения.
Начиная с 0 ≤λ< 1, применяя фактор эквивалентно взвешиванию более старой ошибки. Когда λ = 1, вся предыдущая ошибка рассматривается равного веса в полной погрешности.
Как λ нуль подходов, прошлые ошибки играют меньшую роль в общем количестве. Например, когда λ = 0.9, алгоритм RLS умножает ошибочное значение от 50 выборок в прошлом фактором затухания 0,950 = 5.15 x 10-3, значительно преуменьшив роль влияния прошлой ошибки на текущей полной погрешности.
Вместо того, чтобы использовать приложение системы идентификации, чтобы продемонстрировать адаптивный алгоритм RLS или модель подавления помех, этот пример использует обратную модель системы идентификации, показанную в здесь.
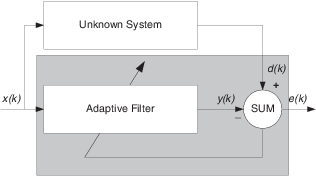
Расположение каскадом адаптивного фильтра с неизвестным фильтром заставляет адаптивный фильтр сходиться к решению, которое является инверсией неизвестной системы.
Если передаточной функцией неизвестного является H (z), и адаптивной передаточной функцией фильтра является G (z), ошибка, измеренная между желаемым сигналом и сигналом от каскадной системы, достигает своего минимума, когда продукт H (z) и G (z) равняется 1, G(z)*H(z) = 1. Для этого отношения, чтобы быть верным, G (z) должен равняться 1/H(z), инверсии передаточной функции неизвестной системы.
Чтобы продемонстрировать, что это верно, создайте сигнал ввести к каскадной паре фильтра.
x = randn(3000,1);
В каскадном случае фильтров неизвестный фильтр приводит к задержке сигнала, прибывающего в точку суммирования после обоих фильтров. Чтобы препятствовать тому, чтобы адаптивный фильтр пытался адаптироваться к сигналу, это еще не видело (эквивалентный предсказанию будущего), задержите желаемый сигнал 32 выборками, порядком неизвестной системы.
Обычно вы не знаете порядка системы, которую вы пытаетесь идентифицировать. В этом случае задержите желаемый сигнал количеством выборок, равных половине порядка адаптивного фильтра. Задержка входа требует предварительного ожидания 12 выборок нулевых значений к x.
delay = zeros(12,1); d = [delay; x(1:2988)]; % Concatenate the delay and the signal.
Необходимо сохранить желаемый сигнальный вектор d та же длина как x, следовательно настроить количество элемента сигнала, чтобы допускать выборки задержки.
Несмотря на то, что не обычно верный, для этого примера вы знаете порядок неизвестного фильтра, таким образом, вы добавляете задержку, равную порядку неизвестного фильтра.
Для неизвестной системы используйте lowpass, КИХ-фильтр 12-го порядка.
ufilt = fir1(12,0.55,'low');
Фильтрация x обеспечивает сигнал входных данных для адаптивной функции алгоритма.
xdata = filter(ufilt,1,x);
Чтобы установить алгоритм RLS, инстанцируйте объекта dsp.RLSFilter и установите его Length, ForgettingFactor и свойства InitialInverseCovariance.
Для получения дополнительной информации о входных условиях подготовить объект алгоритма RLS, обратитесь к dsp.RLSFilter.
p0 = 2 * eye(13); lambda = 0.99; rls = dsp.RLSFilter(13,'ForgettingFactor',lambda,... 'InitialInverseCovariance',p0);
Большая часть процесса к этой точке совпадает с предыдущими примерами. Однако, поскольку этот пример стремится разработать обратное решение, необходимо быть осторожными, о котором сигнал несет данные и который является желаемым сигналом.
Более ранние примеры адаптивных фильтров используют отфильтрованный шум в качестве желаемого сигнала. В этом случае отфильтрованный шум (xdata) несет неизвестную информацию о системе. С Распределением Гаусса и отклонением 1, неотфильтрованный шумовой d является желаемым сигналом. Код, чтобы запустить этот адаптивный пример фильтра
[y,e] = rls(xdata,d);
где y возвращает отфильтрованный выходной параметр, и e содержит сигнал ошибки, когда фильтр адаптируется, чтобы найти инверсию неизвестной системы. Чтобы просмотреть предполагаемый коэффициент фильтра RLS, введите rls.Coefficients.
Следующая фигура представляет результаты адаптации. График содержит кривые отклика значения для неизвестных и адаптированных фильтров. Как напоминание, неизвестный фильтр был фильтром lowpass с сокращением в 0,55 в нормированной шкале частоты от 0 до 1.
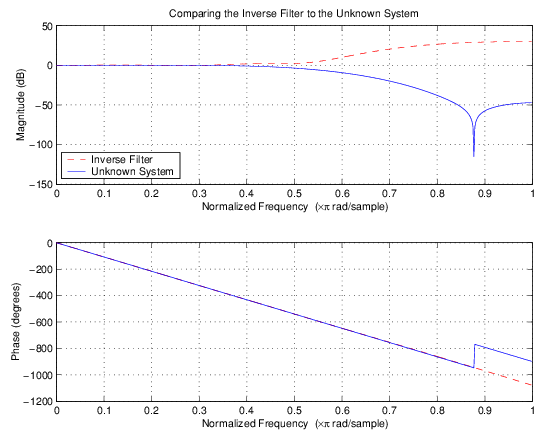
Просматриваемый один (относятся к следующей фигуре), обратная система похожа на справедливый компенсатор для неизвестного фильтра lowpass — фильтр высоких частот с линейной фазой.
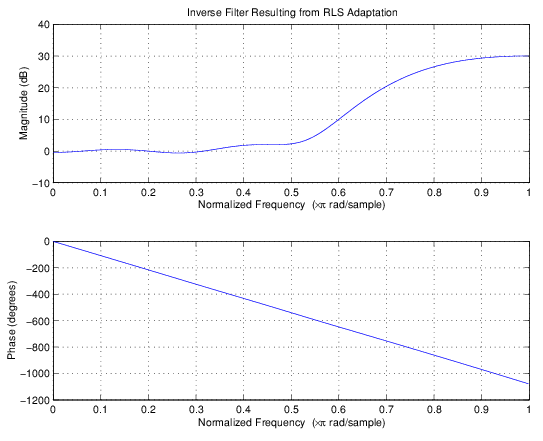
[1] Hayes, Монсон Х., статистическая цифровая обработка сигналов и Modeling, John Wiley & Sons, 1996, 493–552.
[2] Haykin, Саймон, адаптивная теория фильтра, Prentice-Hall, Inc., 1996.