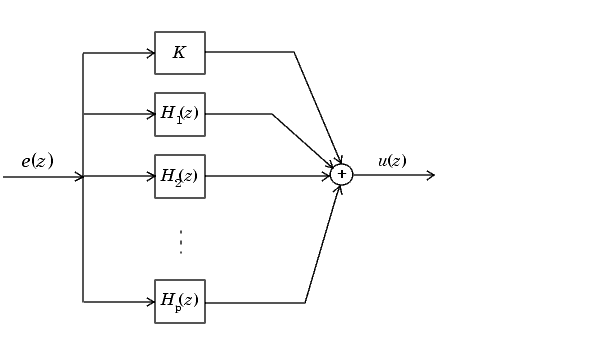
В канонической параллельной форме передаточная функция H (z) расширен в элементарные дроби. H (z) затем понят как сумма константы, и передаточных функций второго порядка первого порядка, как показано:
Это расширение, где K является константой и Hi (z), является первым - и передаточные функции второго порядка, следует.
Как в серийной канонической форме, нет никакого уникального описания для передаточной функции второго порядка и первого порядка. Из-за природы блока Sum не имеет значения упорядоченное расположение отдельных фильтров. Однако из-за постоянного K, можно выбрать передаточные функции второго порядка и первого порядка, таким образом, что их формы более просты, чем те для серийной каскадной формы, описанной в предыдущем разделе. Это сделано путем расширения H (z) как
Схема первого порядка для H (z) следует.
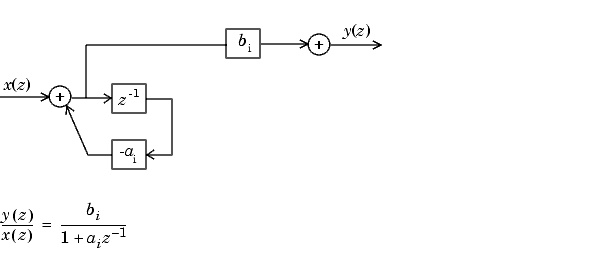
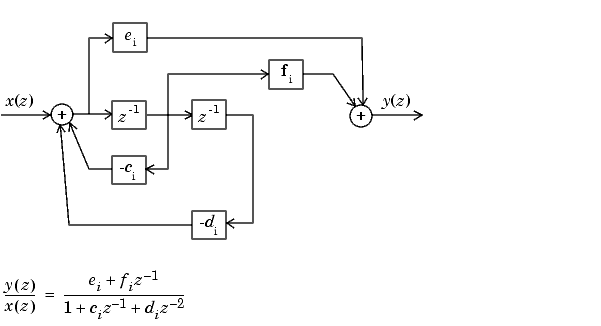
Схема второго порядка для H (z) следует.
Параллельной передаточной функцией формы в качестве примера дают
Реализацию Hex (z) с помощью фиксированной точки, которую блокирует Simulink®, показывают в следующей фигуре. Можно отобразить эту модель путем ввода
fxpdemo_parallel_form
в командной строке MATLAB®.