В канонической серийной каскадной форме передаточная функция H (z) записан как продукт передаточных функций второго порядка и первого порядка:
Это уравнение приводит к канонической серийной каскадной форме.
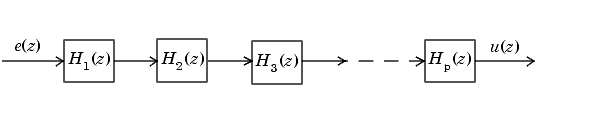
Включая H (z) в Hi (z), где i = 1,2,3..., p может быть сделан различными способами. Используя полюса и нули H (z), можно получить Hi (z) путем группировки пар сопряженных комплексных полюсов и пар сопряженных комплексных нулей, чтобы произвести передаточные функции второго порядка, или путем группировки действительных полюсов и действительных нулей, чтобы произвести или передаточные функции второго порядка или первого порядка. Вы могли также сгруппировать два действительных нуля с парой сопряженных комплексных полюсов или наоборот. С тех пор существует много способов получить Hi (z), необходимо сравнить различные группировки, чтобы видеть, который приводит к лучшим результатам для передаточной функции на рассмотрении.
Например, одна факторизация H (z) может быть
Необходимо также учесть, что упорядоченное расположение отдельного Hi (z) приведет к системам с различными числовыми характеристиками. Вы можете хотеть попробовать различные упорядоченные расположения за данный набор Hi (z), чтобы определить, который дает лучшие числовые характеристики.
Схема первого порядка для H (z) следует.
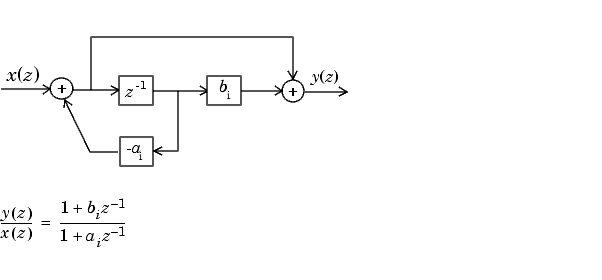
Схема второго порядка для H (z) следует.
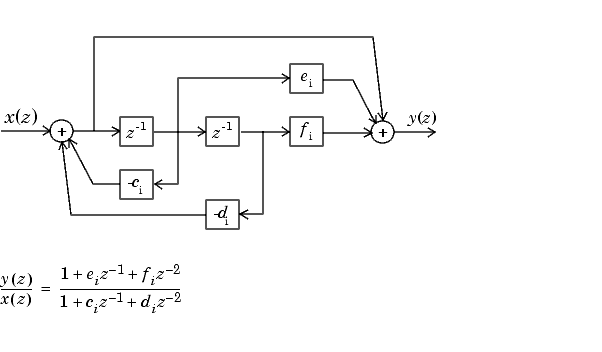
Серийной каскадной передаточной функцией формы в качестве примера дают
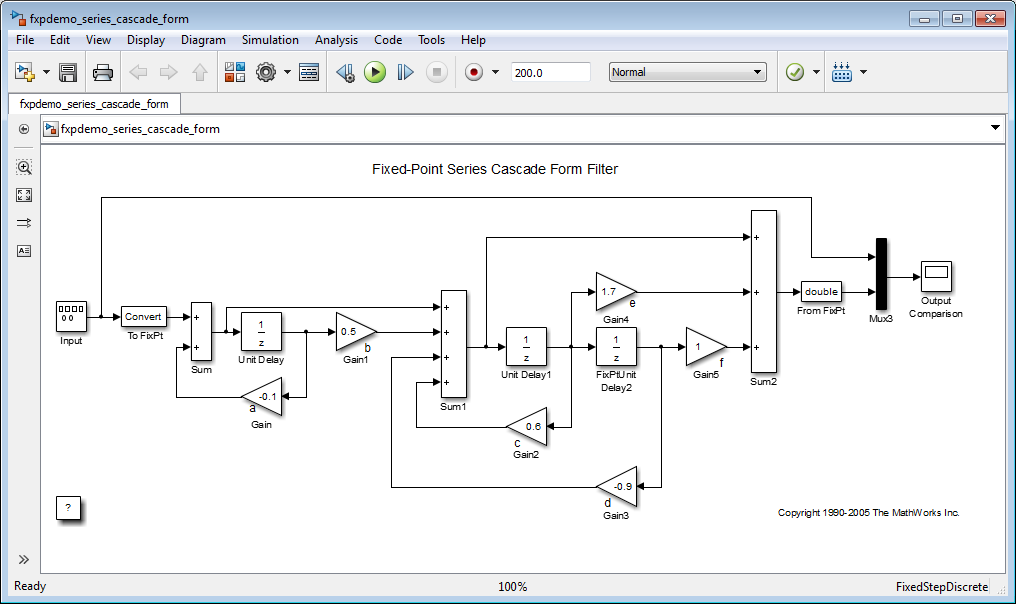
Реализацию Hex (z) с помощью фиксированной точки, которую блокирует Simulink®, показывают в следующей фигуре. Можно отобразить эту модель путем ввода
fxpdemo_series_cascade_form
в командной строке MATLAB®.