Линейная и Нелинейная Ограниченная Минимизация Используя patternsearch

Линейная и нелинейная ограниченная минимизация Используя `patternsearch`

Линейно ограниченная проблема

Описание проблемы

Этот раздел представляет пример выполнения поиска шаблона на ограниченной проблеме минимизации. Пример минимизирует функцию

$F (x) = \frac{}{12} x^{T} H x + f^{T} x,$

где

$\begin{matrix} H = [\begin{matrix} 36 & 17 & 19 & 12 & 8 & 15 \\ 17 & 33 & 18 & 11 & 7 & 14 \\ 19 & 18 & 43 & 13 & 8 & 16 \\ 12 & 11 & 13 & 18 & 6 & 11 \\ 878698 \\ 15 & 14 & 16 & 11 & 8 & 29 \end{matrix}], \\ f = [\begin{matrix} 20 & 15 & 21 & 18 & 29 & 24 \end{matrix}], \end{matrix}$

подвергните ограничениям

$\begin{matrix} A \cdot x \leq b, \\ A e q \cdot x = b e q, \end{matrix}$

где

$\begin{matrix} A = [\begin{matrix} - 8 & 73 & - 4 & 90 \end{matrix}], \\ b = 7, \\ A e q = [\begin{matrix} 71833350 & - 5 & 1 & - 5 & 8 \\ - 2 & - 6 \\ 71191 & - 1 & 2 & - 2 & 3 & - 3 \end{matrix}], \\ b e q = [\begin{matrix} 84 & 62 & 65 & 1 \end{matrix}] . \end{matrix}$

Выполнение поиска шаблона на примере

Чтобы выполнить поиск шаблона на примере, сначала войдите

optimtool('patternsearch')

открыть приложение Оптимизации, или ввести optimtool и затем выбрать patternsearch из меню Solver. Затем введите следующую функцию в поле Objective function:

@lincontest7

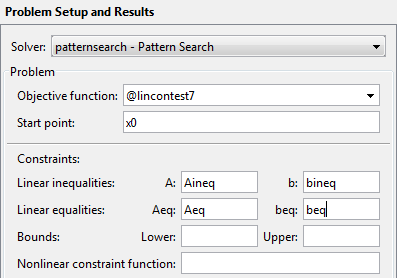
lincontest7 является файлом, включенным в программное обеспечение Global Optimization Toolbox, которое вычисляет целевую функцию для примера. Поскольку матрицы и векторы, задающие отправную точку и ограничения, являются большими, более удобно установить их значения как переменные в рабочей области MATLAB^® сначала и затем ввести имена переменных в приложение Оптимизации. Для этого войдите

x0 = [2 1 0 9 1 0];
Aineq = [-8 7 3 -4 9 0];
bineq = 7;
Aeq = [7 1 8 3 3 3; 5 0 -5 1 -5 8; -2 -6 7 1 1 9; 1 -1 2 -2 3 -3];
beq = [84 62 65 1];

Затем введите следующее в приложение Оптимизации:

Установите Start point на x0.
Установите следующий Linear inequalities:
- Установите A на Aineq.
- Установите b на bineq.
- Установите Aeq на Aeq.
- Установите beq на beq.

Следующие данные показывают эти настройки в приложении Оптимизации.

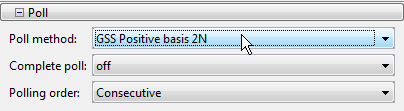
Поскольку это - линейно ограниченная проблема, установите Poll method на GSS Positive basis 2N. Для получения дополнительной информации об эффективности методов поиска GSS для линейно ограниченных проблем, смотрите, Сравнивают Эффективность Опций Опроса.

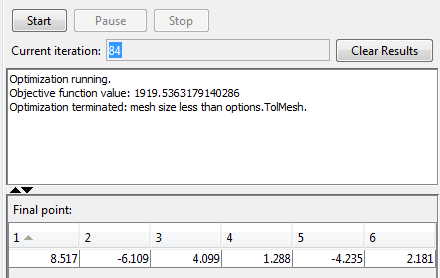
Затем нажмите Start, чтобы запустить поиск шаблона. Когда поиск закончен, результаты отображены в панели Run solver and view results, как показано в следующей фигуре.

Запускать эту проблему с помощью функций командной строки:

x0 = [2 1 0 9 1 0];
Aineq = [-8 7 3 -4 9 0];
bineq = 7;
Aeq = [7 1 8 3 3 3; 5 0 -5 1 -5 8; -2 -6 7 1 1 9; 1 -1 2 -2 3 -3];
beq = [84 62 65 1];
options = optimoptions('patternsearch',...
    'PollMethod','GSSPositiveBasis2N');
[x,fval,exitflag,output] = patternsearch(@lincontest7,x0,... 
   Aineq,bineq,Aeq,beq,[],[],[],options);

Просмотрите решение, значение целевой функции и количество функциональных оценок во время процесса решения.

x,fval,output.funccount

x =

    8.5165   -6.1094    4.0989    1.2877   -4.2348    2.1812


fval =

   1.9195e+03


ans =

   758

Нелинейно ограниченная проблема

Предположим, что вы хотите минимизировать простую целевую функцию двух переменных x1 и x2,

$\min_{x} f (x) = (4 - 2.1 x_{1}^{2} - x_{1}^{4 / 3}) x_{1}^{2} + x_{1} x_{2} + (- 4 + 4 x_{2}^{2}) x_{2}^{2}$

подвергните следующим нелинейным ограничениям неравенства и границам

$\begin{array}{l} x_{1} x_{2} + x_{1} - x_{2} + 1.5 \leq 0 & (нелинейное ограничение) \\ 10 - x_{1} x_{2} \leq 0 & (нелинейное ограничение) \\ 0 \leq x_{1} \leq 1 & (связанный) \\ 0 \leq x_{2} \leq 13 & (связанный) \end{array}$

Начните путем создания ограничительных функций и цели. Во-первых, создайте файл с именем simple_objective.m можно следующим образом:

function y = simple_objective(x)
y = (4 - 2.1*x(1)^2 + x(1)^4/3)*x(1)^2 + x(1)*x(2) + (-4 + 4*x(2)^2)*x(2)^2;

Решатель поиска шаблона принимает, что целевая функция возьмет один вход x, где x имеет столько же элементов сколько количество переменных в проблеме. Целевая функция вычисляет значение функции и возвращает то скалярное значение в его одном возвращаемом аргументе y.

Затем создайте файл с именем simple_constraint.m, содержащий ограничения:

function [c, ceq] = simple_constraint(x)
c = [1.5 + x(1)*x(2) + x(1) - x(2);
-x(1)*x(2) + 10];
ceq = [];

Решатель поиска шаблона принимает, что ограничительная функция возьмет один вход x, где x имеет столько же элементов сколько количество переменных в проблеме. Ограничительная функция вычисляет значения всех ограничений неравенства и равенства и возвращает два вектора, c и ceq, соответственно.

Затем, чтобы минимизировать целевую функцию с помощью функции patternsearch, необходимо передать в указателе на функцию целевой функции, а также определению стартовой точки в качестве второго аргумента. Нижние и верхние границы обеспечиваются как LB и UB соответственно. Кроме того, также необходимо передать указатель на функцию нелинейной ограничительной функции.

ObjectiveFunction = @simple_objective;
X0 = [0 0];   % Starting point
LB = [0 0];   % Lower bound
UB = [1 13];  % Upper bound
ConstraintFunction = @simple_constraint;
[x,fval] = patternsearch(ObjectiveFunction,X0,[],[],[],[],...
                         LB,UB,ConstraintFunction)

Optimization terminated: mesh size less than options.MeshTolerance
 and constraint violation is less than options.ConstraintTolerance.

x =
    0.8122   12.3122

fval =
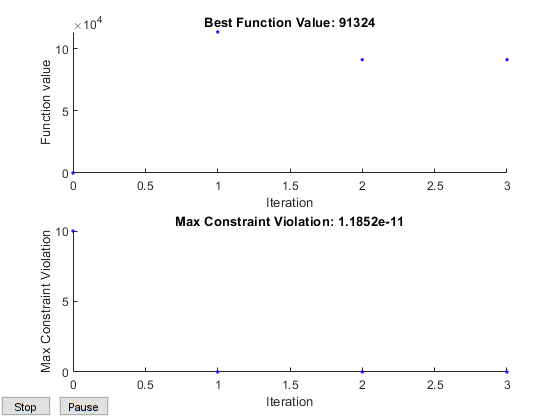
  9.1324e+004

Затем, постройте результаты. Создайте опции с помощью optimoptions, который выбирает две функции построения графика. Первая функция построения графика psplotbestf строит лучшее значение целевой функции в каждой итерации. Вторая функция построения графика psplotmaxconstr строит максимальное ограничительное нарушение в каждой итерации.

Примечание

Можно также визуализировать прогресс алгоритма путем отображения информации к Командному окну с помощью опции 'Display'.

options = optimoptions('patternsearch','PlotFcn',{@psplotbestf,@psplotmaxconstr},'Display','iter');
[x,fval] = patternsearch(ObjectiveFunction,X0,[],[],[],[],LB,UB,ConstraintFunction,options)

                                      Max
  Iter   Func-count       f(x)      Constraint   MeshSize      Method
    0         1            0           10       0.8919    
    1        28       113580            0        0.001   Increase penalty
    2       105        91324    1.776e-07        1e-05   Increase penalty
    3       192        91324    1.185e-11        1e-07   Increase penalty
Optimization terminated: mesh size less than options.MeshTolerance
 and constraint violation is less than options.ConstraintTolerance.

x =

    0.8122   12.3122


fval =

   9.1324e+04

Лучшее значение целевой функции и максимальное ограничительное нарушение в каждой итерации

Документация