Определенные функции Mapping Toolbox™ вычисляют основные географические меры для пространственного анализа и для фильтрации и подготовки данных. Поскольку функции MATLAB® могут вычислить статистику, такую как средние значения, медианы, и отклонения, почему бы не использовать те функции в тулбоксе? В первую очередь, классические статистические формулы обычно принимают, что данные одномерны (и, часто, нормально распределены). Поскольку это не верно для картографических данных, пространственные аналитики разработали статистические меры, которые расширяют обычную статистику к более высоким размерностям.
Во-вторых, такие формулы обычно принимают, что данные занимают двумерную Декартову систему координат. Вычислительная статистика для картографических данных с географическими координатами, как будто это было в Декартовой среде, может дать статистически несоответствующие результаты. В то время как это предположение может иногда приводить к разумным числовым приближениям в небольших географических областях, для больших областей оно может привести к неправильным заключениям из-за мер по расстоянию и предположений области, которые являются несоответствующими для сфер и сфероидов. Функции Mapping Toolbox соответственно вычисляют статистику для картографических данных, избегая этих потенциальных ловушек.
Рассмотрите проблему вычисления среднего положения набора географических точек. Взятие среднего арифметического широт и долгот с помощью стандартного MATLAB, функция mean может казаться разумной, но выполнение этого могло привести к вводящим в заблуждение результатам.
Возьмите две точки в той же широте, на расстоянии в 180 ° в долготе, например (30°N, 90°W) и (30°N, 90°E). Средняя широта (30+30)/2=30, который кажется правильным. Точно так же средняя долгота должна быть (90 + (-90)),/2=0. Однако как можно также выразить 90°W как 270°E, (90+270),/2=180 является также допустимой средней долготой. Таким образом существует два правильных ответа, главный меридиан и линия перемены даты. Это демонстрирует, как шарообразность Земли вводит тонкость в пространственную статистику.
Эта проблема является далее сложной, когда некоторые точки в различных широтах. Поскольку степень долготы в Северном полярном круге преодолевает намного меньшую дистанцию, чем степень на экватор, расстояние между точками, имеющими данное различие в долготе, отличается широтой.
На самом деле 30°N правильная средняя широта в первом примере? Среднее положение двух точек должно быть равноотстоящим от тех двух точек и должно также минимизировать общее расстояние. (30°N, 0 °) удовлетворяют эти критерии?
dist1 = distance(30,90,30,0) dist1 = 75.5225 dist2 = distance(30,-90,30,0) dist2 = 75.5225
Рассмотрите третий вопрос, (lat, lon), который является также равноотстоящим от вышеупомянутых двух точек, но на меньшем расстоянии:
dist1 = distance(30,90,lat,lon) dist1 = 60.0000 dist2 = distance(30,-90,lat,lon) dist2 = 60.0000
Какова эта таинственная точка? lat 90°N, и любой lon сделает. Северный полюс является истинным географическим средним значением этих двух точек. Обратите внимание на то, что большой круг, содержащий обе точки, пробегает Северный полюс (большой круг представляет кратчайший путь между двумя точками на сфере).
Функция Mapping Toolbox meanm определяет географическое среднее значение любого числа точек. Это делает это использующее 3D векторное сложение всех точек. Например, попробуйте следующее:
lats = [30 30]; longs = [-90 90]; [latbar,longbar] = meanm(lats,longs) latbar = 90 longbar = 0
Это - ответ, который вы теперь ожидаете. Это географическое среднее значение может привести к одной причуде; если векторы, все отменяют друг друга, среднее значение, являются центром планеты. В этом случае возвращенная средняя точка (NaN,NaN), и предупреждение выведено. Это явление является очень невероятным в действительных данных, но может быть легко создано. Например, происходит, когда все точки равномерно распределены вдоль большого круга. Попытайтесь брать географическое среднее значение (0 °, 0 °), (0 °, 120 °), и (0 °, 240 °), которые делят на три равные части экватор.
elats = [0 0 0];
elons = [60 120 240];
meanm(elats, elons)
ans =
0 120.0000Как вы можете теперь ожидать, Декартово определение стандартного отклонения, обеспеченного в стандартной функции MATLAB, std является также несоответствующим для географических данных, которые не спроектированы или покрывают значительный фрагмент планеты. В зависимости от вашей цели вы можете хотеть использовать отдельные географические отклонения для широты и долготы, обеспеченной функциональным stdm или одним стандартным расстоянием, обеспеченным в stdist. Оба метода измеряют отклонение точек от среднего положения, вычисленного meanm.
Указатели на функцию stdm отклонения широты и долготы отдельно.
[latstd,lonstd] = stdm(lat,lon)
Функция возвращает два отклонения, один для широт и один для долгот.
Отклонение широты является прямым вычислением стандартного отклонения от средней широты (средняя параллель) возвращенный meanm. Это - разумная мера для большинства случаев, поскольку на сфере, по крайней мере, степень широты всегда имеет ту же длину дуги.
Отклонение долготы является другим вопросом. Простые вычисления на основе суммы квадратов угловое отклонение от средней долготы (средний меридиан) вводят в заблуждение. Длина дуги, представленная степенью долготы в экстремальных широтах, значительно меньше, чем это в низких широтах.
Термин отъезд используется, чтобы представлять расстояние длины дуги вдоль параллели точки от данного меридиана. Например, принимая сферическую планету, отъезд степени долготы на экватор является степенью длины дуги, но отъезд степени долготы в широте 60 ° является половиной степени длины дуги. Функция stdm вычисляет исходное отклонение суммы квадратов от среднего меридиана.
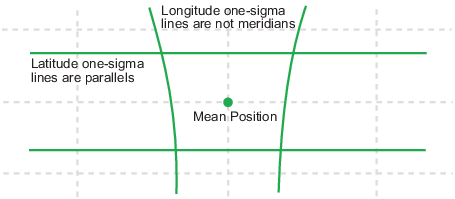
Если вы хотите построить графики с одной сигмой для stdm, строки сигмы широты являются параллелями. Однако строки сигмы долготы не являются меридианами; они - строки постоянного отклонения от средней параллели.
Эта обработка отклонения имеет свои проблемы. Например, его зависимость от логики системы координат может заставить его ломаться около полюсов. Поэтому стандартное расстояние, обеспеченное stdist, часто является лучшей мерой отклонения. Обработка stdm полезна для многих приложений, особенно когда данные не являются глобальной переменной. Например, эти потенциальные трудности не были бы опасностью для точек данных, ограниченных страной Мексика.
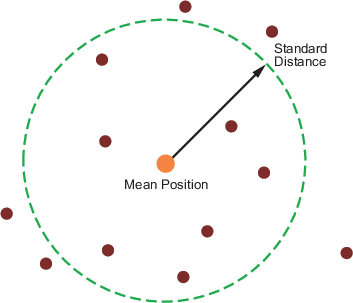
Стандартное расстояние географических данных является мерой дисперсии данных с точки зрения его расстояния от географического среднего значения. Среди его преимуществ его применимость где угодно на земном шаре и его одно значение:
dist = stdist(lat,lon)
Короче говоря, стандартное расстояние является средним значением, нормой или кубической нормой расстояний точек данных в большом круговом смысле от среднего положения. Это - вероятно, превосходящая мера к этим двум отклонениям, возвращенным stdm кроме тех случаев, когда особенно широта - или зависимая долготой функция является объектом исследования.