Чтобы ввести коэффициенты для вашего УЧП, выберите PDE > PDE Specification.
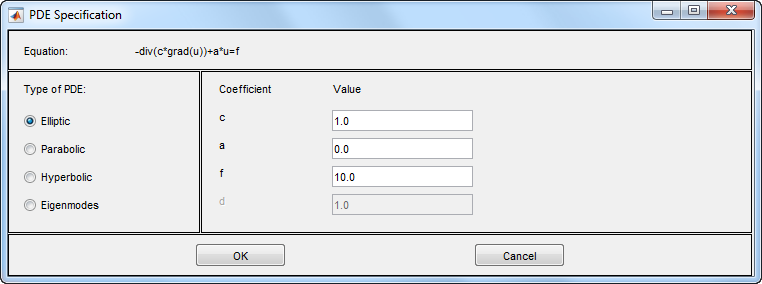
Введите текстовые выражения с помощью этих соглашений:
x — x - координата
y — y - координата
u Решение уравнения
ux — производная u в x - направление
uy — производная u в y - направление
t Время (параболические и гиперболические уравнения)
sd — Номер субдомена
Например, вы могли использовать это выражение, чтобы представлять коэффициент:
(x + y)./(x.^2 + y.^2 + 1) + 3 + sin(t)./(1 + u.^4)
Для эллиптических проблем, когда вы включаете u, ux или uy, необходимо использовать нелинейный решатель. Выберите Solve > Parameters > Use nonlinear solver.
Не используйте кавычки или ненужные пробелы в ваших записях. Синтаксический анализатор может неправильно истолковать пробел как векторный разделитель, как тогда, когда вектор MATLAB® использует пространство, чтобы разделить элементы вектора.
Используйте .*, ./ и .^ для умножения, деления и операций возведения в степень. Текстовые выражения работают с векторами - строками, таким образом, операции должны быть целесообразными для векторов - строк. Векторы - строки являются значениями в треугольных центроидах в mesh.
Можно записать функции MATLAB для выражений простого текста, а также коэффициентов. Например, предположите свой коэффициент, f дан файлом fcoeff.m.
function f = fcoeff(x,y,t,sd) f = (x.*y)./(1 + x.^2 + y.^2); % f on subdomain 1 f = f + log(1 + t); % include time r = (sd == 2); % subdomain 2 f2 = cos(x + y); % coefficient on subdomain 2 f(r) = f2(r); % f on subdomain 2
Используйте fcoeff(x,y,t,sd) в качестве коэффициента f в решателе parabolic.
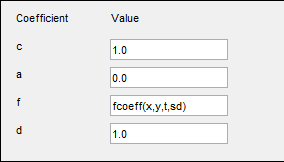
Коэффициент c является матрицей 2 на 2. Можно дать 1-, 2-, 3-, или матричные выражения с 4 элементами. Разделите выражения для элементов пробелами. Эти выражения среднее значение:
Выражение с 1 элементом:
Выражение с 2 элементами:
Выражение с 3 элементами:
Выражение с 4 элементами:
Например, c является симметрической матрицей с постоянными диагональными элементами и cos(xy) как недиагональные условия:
1.1 cos(x.*y) 5.5
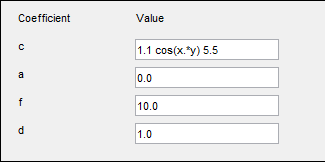
Это соответствует коэффициентам для параболического уравнения