Общее сопротивление в тепловом жидком ответвлении
Simscape / Библиотека Основы / Тепловая Жидкость / Элементы

Блок Flow Resistance (TL) моделирует общий перепад давления в тепловом жидком сетевом ответвлении. Перепад давления пропорционален квадрату массовой скорости потока жидкости. Коэффициент пропорциональности определяется от номинальных условий работы, заданных в диалоговом окне блока.
Используйте этот блок, когда единственные доступные данные для компонента будут его перепадом давления как функцией его массовой скорости потока жидкости. Объедините блок с другими, чтобы создать собственный компонент, который более точно получает перепад давления, который он вызывает — например, теплообменник на основе блока камеры.
Объем жидкости в сопротивлении потока принят, чтобы быть незначительным. Массовая скорость потока жидкости в через один порт должна затем точно равняться массовой скорости потока жидкости через другой порт:
где и заданы как массовые скорости потока жидкости на компонент через порты A и B, соответственно.
Энергия может ввести и оставить сопротивление потока через тепловые жидкие порты только. Никакой теплообмен не происходит между стеной и средой. Кроме того, никакие не работают, сделан на или жидкостью. Энергетическая скорость потока жидкости в через один порт должна затем точно равняться энергетической скорости потока жидкости через другой порт:
где ϕ A и ϕ B является энергетическими скоростями потока жидкости в сопротивление потока через порты A и B.
Соответствующие внешние силы на жидкости включают тех из-за давления в портах и тех из-за вязкого трения в стенах компонента. Сила тяжести проигнорирована, как другие массовые силы. При выражении фрикционных сил с точки зрения коэффициента потерь ξ приводит к полуэмпирическому выражению:
где:
Δp является перепадом давления от порта к порту B — то есть, p + p B.
ξ является коэффициентом потерь.
ρ является жидкой плотностью.
S является областью потока.
Уравнение перепада давления реализовано с двумя модификациями. Во-первых, чтобы позволить для разнообразия в знаке после реверсирования направления потока, это переписано:
где перепад давления положителен, только если массовая скорость потока жидкости также. Во-вторых, чтобы устранить особенности, должные течь реверсирование — особенности, которые могут поставить проблему перед числовыми решателями во время симуляции — она линеаризуется в небольшой области почти нулевого потока:
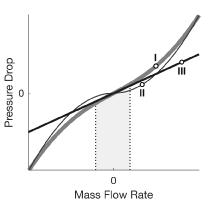
где пороговая скорость потока жидкости массы, ниже которой линеаризуется перепад давления. Данные показывают измененный перепад давления против локальной массовой скорости потока жидкости (изогнитесь I):
Выше , перепад давления аппроксимирует, который выразил в исходном уравнении (изогнитесь II), и это меняется . Эта зависимость соразмерна с наблюдаемым в турбулентных течениях.
Ниже , перепад давления аппроксимирует прямую линию с наклоном, частично зависящим от (изогнитесь III), и это меняется . Эта зависимость соразмерна с наблюдаемым в ламинарных течениях.
Для простоты моделирования коэффициент потерь ξ не требуется как параметры блоков. Вместо этого это автоматически вычисляется из номинального условия, заданного в диалоговом окне блока:
где звездочка (*) обозначает значение в номинальных условиях работы. Лежание в основе всех этих вычислений является предположением что пороговая скорость потока жидкости массы намного меньше, чем номинальная стоимость . Заменяя дробный ξ / (2S2) в выражении для урожаев перепада давления:
или, эквивалентно:
где C является коэффициентом пропорциональности между перепадом давления через сопротивление потока и локальной массовой скоростью потока жидкости. Это задано как:
Если жидкая массовая плотность обработана как инвариант, то его номинальная стоимость и фактические значения должны всегда быть равными. Это - предположение, сделанное в блоке. Отношением этих двух является затем всегда 1, и дробный C/ρ уменьшает до:
С точки зрения постоянного K итоговое уравнение перепада давления: