Задайте область значений и уровень изменения неопределенных или изменяющихся во времени параметров
pv = pvec('box',range,rates)
pv = pvec('pol',vertices)
pvec используется в сочетании с psys, чтобы задать зависимые параметром системы. Такие системы параметризованы векторным p = (p 1..., pn) неопределенного или изменяющегося во времени действительного parameters pi. Функциональный pvec задает область значений значений и уровни изменения этих параметров.
Тип 'box' соответствует независимым параметрам, располагающимся в интервалах
Вектор параметра p затем принимает значения в гиперпрямоугольнике Rn, вызвал поле параметра. Второй областью значений аргумента является n-by-2 матрица, которая складывает экстремальные значения и из каждого pj. Если третий аргумент rates не использован, все параметры приняты независимые от времени. В противном случае rates является также n-by-2 матрица, и ее j-th строка задает нижние и верхние границы и на :
Набор = –Inf и = Inf, если pj (t) может отличаться произвольно быстро или с перерывами.
Тип 'pol' соответствует векторам параметра p, располагающийся в многограннике пространства параметров Rn. Этот многогранник задан набором вершин V 1, . . ., Vn соответствие “экстремальным” значениям векторного p. Такие векторы параметра объявляются командой
pv = pvec('pol',[v1,v2, . . ., vn])
где второй аргумент является конкатенацией векторов v1,...,vn.
Выходным аргументом pv является структурированная матрица, хранящая описание вектора параметра. Используйте pvinfo, чтобы считать содержимое pv.
Рассмотрите проблему с двумя независимыми от времени параметрами
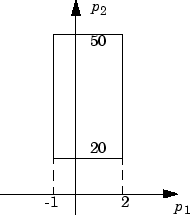
p 1 ∊ [–1, 2], p 2 ∊ [20, 50]
Соответствующий вектор параметра p = (p 1, p 2) задан
pv = pvec('box',[-1 2;20 50])
Также этот вектор может рассматриваться как принимающие значения в прямоугольнике, чертившем в следующей фигуре. Четыре угла этого прямоугольника являются этими четырьмя векторами
Следовательно, вы могли также задать p
pv = pvec('pol',[v1,v2,v3,v4])
Поле Parameter