Соответствуйте обобщенной линейной модели Смешанных Эффектов

Этот пример показывает, как соответствовать обобщенной линейной модели смешанных эффектов (GLME) к выборочным данным.

Загрузите выборочные данные.
Соответствуйте модели GLME и интерпретируйте результаты.
Проверяйте значение случайного эффекта.
Сравните две модели.
Постройте график результатов.

Загрузите выборочные данные.

load mfr

Компания-производитель управляет 50 фабриками во всем мире, и каждый запускает процесс пакетной обработки, чтобы создать готовое изделие. Компания хочет сократить число дефектов в каждом пакете, таким образом, это разработало новый производственный процесс. Однако компания хочет протестировать новый процесс на избранных фабриках, чтобы гарантировать, что это эффективно перед развертыванием его ко всем 50 местам.

Чтобы протестировать, сокращает ли новый процесс значительно количество дефектов в каждом пакете, компания выбрала 20 своих фабрик наугад, чтобы участвовать в эксперименте. Десять фабрик реализовали новый процесс, в то время как другие десять использовали старый процесс.

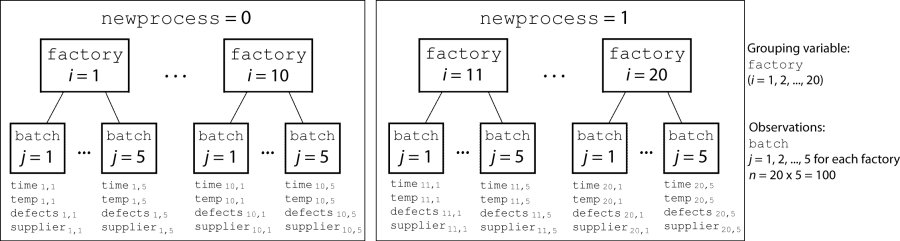
На каждой из этих 20 фабрик (i = 1, 2..., 20), компания запустила пять пакетов (j = 1, 2..., 5) и записала следующие данные в таблице mfr:

Отметьте, чтобы указать на использование нового процесса:
- Если пакет использовал новый процесс, то newprocess = 1
- Если пакет использовал старый процесс, то newprocess = 0
Время вычислений для пакета, в часах (time)
Температура пакета, в градусах Цельсия (temp)
Поставщик химиката использовал в пакете (supplier)
- supplier является категориальной переменной с уровнями A, B и C, где каждый уровень представляет одного из этих трех поставщиков
Количество дефектов в пакете (дефекты)

Данные также включают time_dev и temp_dev, которые представляют абсолютное отклонение времени и температуры, соответственно, из стандарта процесса 3 часов и 20 градусов Цельсия. Переменная отклика defects имеет распределение Пуассона. Это - моделируемые данные.

Компания хочет определить, сокращает ли новый процесс значительно количество дефектов в каждом пакете при составлении качественных различий, которые могут существовать из-за специфичных для фабрики изменений вовремя, температуры и поставщика. Количество дефектов на пакет может быть смоделировано с помощью Ядовитого распределения:

$d e f e c t s_{i j} ~ P o i s s o n (μ_{i j})$

Используйте обобщенную линейную модель смешанных эффектов, чтобы смоделировать количество дефектов на пакет:

$\begin{array}{l} журнал (μ_{i j}) = β_{0} + β_{1} n e w p r o c e s s_{i j} + β_{2} t i m e_d e v_{i j} \\ + β_{3} t e m p_d e v_{i j} + β_{4} s u p p l i e r_C_{i j} + β_{5} s u p p l i e r_B_{i j} + b_{i}, \end{array}$

где

_defectsij является количеством дефектов, наблюдаемых в пакете, произведенном фабрикой i во время пакетного j.
_μij является средним количеством дефектов, соответствующих фабрике i (где i = 1, 2..., 20) во время пакетного j (где j = 1, 2..., 5).
_newprocessij, _{time_devij} и _{temp_devij} являются измерениями для каждой переменной, которые соответствуют фабрике i во время пакетного j. Например, _newprocessij указывает, использовал ли пакет, произведенный фабрикой i во время пакетного j, новый процесс.
_{supplier_Cij} и _{supplier_Bij} являются фиктивными переменными, которые используют эффекты (сумма к нулю), кодирование, чтобы указать или компания C или B, соответственно, предоставило химикаты процесса для пакета, произведенного фабрикой i во время пакетного j.
_bi ~ N (0, _σb ²) является прерыванием случайных эффектов для каждой фабрики i, который составляет специфичное для фабрики изменение по качеству.

Соответствуйте модели GLME и интерпретируйте результаты.

Соответствуйте обобщенной линейной модели смешанных эффектов использование newprocess, time_dev, temp_dev и supplier как предикторы фиксированных эффектов. Включайте термин случайных эффектов для прерывания, сгруппированного factory, чтобы составлять качественные различия, которые могут существовать из-за специфичных для фабрики изменений. Переменная отклика defects имеет распределение Пуассона и соответствующую функцию ссылки для этой модели, является журналом. Используйте подходящий метод Лапласа, чтобы оценить коэффициенты. Задайте фиктивную переменную, кодирующую как 'effects', таким образом, фиктивная переменная содействующая сумма к 0.

glme = fitglme(mfr,...
'defects ~ 1 + newprocess + time_dev + temp_dev + supplier + (1|factory)',...
'Distribution','Poisson','Link','log','FitMethod','Laplace',...
'DummyVarCoding','effects')

glme = 


Generalized linear mixed-effects model fit by ML

Model information:
    Number of observations             100
    Fixed effects coefficients           6
    Random effects coefficients         20
    Covariance parameters                1
    Distribution                    Poisson
    Link                            Log   
    FitMethod                       Laplace

Formula:
    defects ~ 1 + newprocess + time_dev + temp_dev + supplier + (1 | factory)

Model fit statistics:
    AIC       BIC       LogLikelihood    Deviance
    416.35    434.58    -201.17          402.35  

Fixed effects coefficients (95% CIs):
    Name                 Estimate     SE          tStat       DF    pValue    
    '(Intercept)'           1.4689     0.15988      9.1875    94    9.8194e-15
    'newprocess'          -0.36766     0.17755     -2.0708    94      0.041122
    'time_dev'           -0.094521     0.82849    -0.11409    94       0.90941
    'temp_dev'            -0.28317      0.9617    -0.29444    94       0.76907
    'supplier_C'         -0.071868    0.078024     -0.9211    94       0.35936
    'supplier_B'          0.071072     0.07739     0.91836    94       0.36078


    Lower        Upper    
       1.1515       1.7864
     -0.72019    -0.015134
      -1.7395       1.5505
      -2.1926       1.6263
     -0.22679     0.083051
    -0.082588      0.22473

Random effects covariance parameters:
Group: factory (20 Levels)
    Name1                Name2                Type         Estimate
    '(Intercept)'        '(Intercept)'        'std'        0.31381 

Group: Error
    Name                      Estimate
    'sqrt(Dispersion)'        1

Таблица Model information показывает общее количество наблюдений в выборочных данных (100), количество фиксированных - и коэффициенты случайных эффектов (6 и 20, соответственно), и количество параметров ковариации (1). Это также указывает, что переменная отклика имеет распределение Poisson, функцией ссылки является Log, и подходящим методом является Laplace.

Formula указывает на образцовую спецификацию с помощью обозначения Уилкинсона.

Статистика отображений таблицы Model fit statistics раньше оценивала качество подгонки модели. Это включает критерий информации о Akaike (AIC), Байесов информационный критерий (BIC) значения, логарифмическая вероятность (LogLikelihood) и отклонение (Deviance) значения.

Таблица Fixed effects coefficients показывает, что fitglme возвратил 95% доверительных интервалов. Это содержит одну строку для каждого предиктора фиксированных эффектов, и каждый столбец содержит статистику, соответствующую тому предиктору. Столбец 1 (Name) содержит имя каждого коэффициента фиксированных эффектов, столбец 2 (Estimate) содержит свою ориентировочную стоимость, и столбец 3 (SE) содержит стандартную погрешность коэффициента. Столбец 4 (tStat) содержит t - статистическая величина для теста гипотезы, что коэффициент равен 0. Столбец 5 (DF) и столбец 6 (pValue) содержит степени свободы и p - значение, которые соответствуют t - статистическая величина, соответственно. Последние два столбца (Lower и Upper) отображают нижние и верхние пределы, соответственно, 95%-го доверительного интервала для каждого коэффициента фиксированных эффектов.

Random effects covariance parameters отображает таблицу для каждой группирующей переменной (здесь, только factory), включая его общее количество уровней (20), и тип и оценка параметра ковариации. Здесь, std указывает, что fitglme возвращает стандартное отклонение случайного эффекта, сопоставленного с предиктором фабрики, который имеет ориентировочную стоимость 0,31381. Это также отображает таблицу, содержащую тип параметра ошибок (здесь, квадратный корень из дисперсионного параметра), и его ориентировочная стоимость 1.

Стандартное отображение, сгенерированное fitglme, не обеспечивает доверительные интервалы для параметров случайных эффектов. Чтобы вычислить и отобразить эти значения, используйте covarianceParameters.

Проверяйте значение случайного эффекта.

Чтобы определить, является ли прерывание случайных эффектов, сгруппированное factory, статистически значительным, вычислите доверительные интервалы для предполагаемого параметра ковариации.

[psi,dispersion,stats] = covarianceParameters(glme);

covarianceParameters возвращает предполагаемый параметр ковариации в psi, предполагаемый дисперсионный параметр dispersion и массив ячеек связанной статистики stats. Первая ячейка stats содержит статистику для factory, в то время как вторая ячейка содержит статистику для дисперсионного параметра.

Отобразите первую ячейку stats, чтобы видеть доверительные интервалы для предполагаемого параметра ковариации для factory.

stats{1}

ans = 


    Covariance Type: Isotropic

    Group      Name1                Name2                Type     
    factory    '(Intercept)'        '(Intercept)'        'std'    


    Estimate    Lower      Upper  
    0.31381     0.19253    0.51148

Столбцы Lower и Upper отображают 95%-й доверительный интервал по умолчанию для предполагаемого параметра ковариации для factory. Поскольку интервал [0.19253,0.51148] не содержит 0, прерывание случайных эффектов является значительным на 5%-м уровне значения. Поэтому случайный эффект из-за специфичного для фабрики изменения должен быть рассмотрен прежде, чем сделать любые выводы об эффективности нового производственного процесса.

Сравните две модели.

Сравните модель смешанных эффектов, которая включает прерывание случайных эффектов, сгруппированное factory с моделью, которая не включает случайный эффект, чтобы определить, какая модель является лучшим пригодным для данных. Соответствуйте первой модели, FEglme, с помощью только предикторы фиксированных эффектов newprocess, time_dev, temp_dev и supplier. Соответствуйте второй модели, glme, с помощью этих тех же предикторов фиксированных эффектов, но также и включая прерывание случайных эффектов, сгруппированное factory.

FEglme = fitglme(mfr,...
'defects ~ 1 + newprocess + time_dev + temp_dev + supplier',...
'Distribution','Poisson','Link','log','FitMethod','Laplace');

glme = fitglme(mfr,...
'defects ~ 1 + newprocess + time_dev + temp_dev + supplier + (1|factory)',...
'Distribution','Poisson','Link','log','FitMethod','Laplace');

Сравните эти две модели с помощью теста отношения правдоподобия. Задайте 'CheckNesting' как true, таким образом, compare возвращает предупреждение, если вложенные требования не удовлетворены.

results = compare(FEglme,glme,'CheckNesting',true)

results = 


    Theoretical Likelihood Ratio Test

    Model     DF    AIC       BIC       LogLik     LRStat    deltaDF
    FEglme    6     431.02    446.65    -209.51                     
    glme      7     416.35    434.58    -201.17    16.672    1      


    pValue    
              
    4.4435e-05

compare возвращает степени свободы (DF), критерий информации о Akaike (AIC), Байесов информационный критерий (BIC) и логарифмические значения вероятности для каждой модели. glme имеет меньший AIC, BIC и логарифмические значения вероятности, чем FEglme, который указывает, что glme (модель, содержащая термин случайных эффектов для прерывания, сгруппированного фабрикой), является лучше подходящей моделью для этих данных. Кроме того, маленький p - значение указывает, что compare отклоняет нулевую гипотезу, что вектор отклика был сгенерирован фиксированными эффектами только модель FEglme, в пользу альтернативы, что вектор отклика был сгенерирован моделью glme смешанных эффектов.

Постройте график результатов.

Сгенерируйте подходящие условные средние значения для модели.

mufit = fitted(glme);

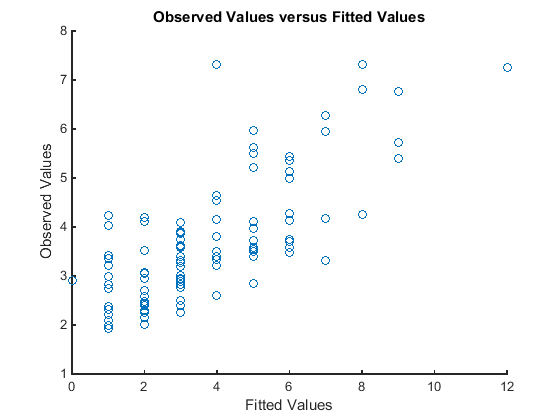
Постройте наблюдаемые значения ответа по сравнению с подходящими значениями ответа.

figure
scatter(mfr.defects,mufit)
title('Observed Values versus Fitted Values')
xlabel('Fitted Values')
ylabel('Observed Values')

Создайте диагностические графики с помощью условного выражения невязки Пирсона для предположений тестовой модели. Поскольку необработанные невязки для обобщенных линейных моделей смешанных эффектов не имеют постоянного отклонения через наблюдения, используют условное выражение невязки Пирсона вместо этого.

Постройте гистограмму, чтобы визуально подтвердить, что среднее значение невязок Пирсона равно 0. Если модель будет правильна, мы ожидаем, что невязки Пирсона будут сосредоточены в 0.

plotResiduals(glme,'histogram','ResidualType','Pearson')

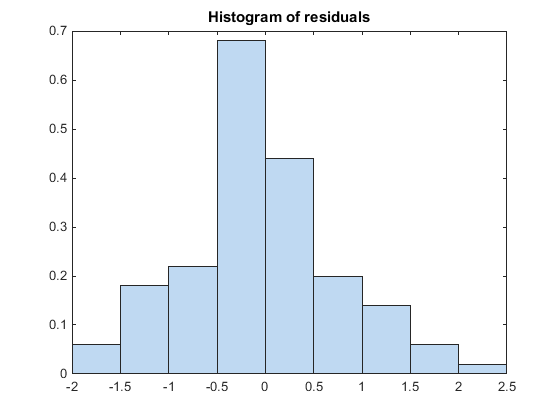
Гистограмма показывает, что невязки Пирсона сосредоточены в 0.

Постройте невязки Пирсона по сравнению с подходящими значениями, чтобы проверять на знаки непостоянного отклонения среди невязок (heteroscedasticity). Мы ожидаем, что условное выражение невязки Пирсона будет иметь постоянное отклонение. Поэтому график условного выражения, невязки Пирсона по сравнению с условным выражением соответствовали значениям, не должен показывать, что любая систематическая зависимость от условного выражения соответствовала значениям.

plotResiduals(glme,'fitted','ResidualType','Pearson')

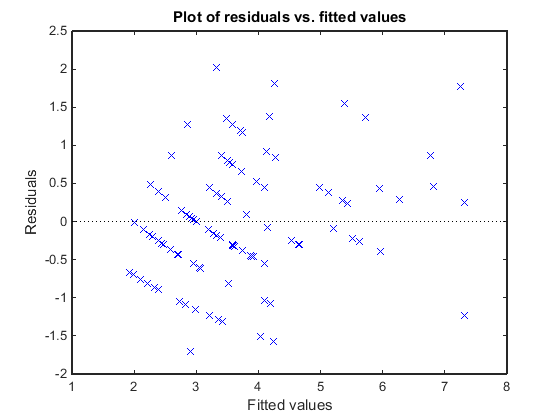
График не показывает систематическую зависимость от подходящих значений, таким образом, нет никаких знаков непостоянного отклонения среди невязок.

Постройте невязки Пирсона по сравнению с изолированными невязками, чтобы проверять на корреляцию среди невязок. Условное предположение независимости в GLME подразумевает, что условное выражение невязки Пирсона является приблизительно некоррелированым.

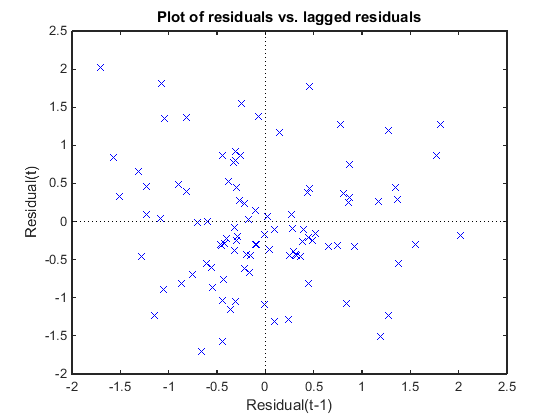
Нет никакого шаблона к графику, таким образом, нет никаких знаков корреляции среди невязок.

Документация