Exponenta Banner

Dom:: Quaternion

Скошенное поле кватернионов

расширьте все на странице

Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.

Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.

Синтаксис

Dom::Quaternion(listi)
Dom::Quaternion(ex)
Dom::Quaternion(M)

Описание

Доменный Dom::Quaternion представляет скошенное поле кватернионов.

Кватернионы обычно задаются, чтобы быть комплексными 2 ×2 матрицы специальной формы

,

где a, b, c, d является вещественными числами. Другим обычным обозначением является a + bi + cj + dk; подполе тех кватернионов, для которых c = d = 0 изоморфен к полю комплексных чисел.

Доменный Dom::Quaternion расценивает эти поля, как являющиеся идентичным, и он позволяет оба обозначения, которые были упомянуты, а также просто [a,b,c,d].

Если вы вводите кватернион как арифметическое выражение ex, идентификаторы i, j, и k понят в упомянутом выше пути; I, J и K могут использоваться альтернативно, и можно также смешать строчные и прописные буквы. Каждое подвыражение ex, не содержащего один из них, должно быть действительным и постоянным.

Примечание

Убедитесь, что вы не присвоили значение одному из упомянутых идентификаторов.

Dom::Quaternion имеет доменный Dom::BaseDomain как свою супер область, т.е. это наследовало каждый метод, который задан Dom::BaseDomain и не повторно реализован Dom::Quaternion. Методы, описанные ниже, повторно реализованы Dom::Quaternion.

Суперобласть

Dom::BaseDomain

Аксиомы

Ax::canonicalRep

Категории

Cat::SkewField

Примеры

Пример 1

Создание некоторых кватернионов.

Dom::Quaternion([1,2,3,4]),
Dom::Quaternion(11+12*i+13*j+14*k);
M := Dom::Matrix(Dom::Complex)([[3+4*I,-6-2*I],[6-2*I,3-4*I]]):
M, Dom::Quaternion(M)

Пример 2

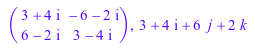
Выполнение некоторой стандартной арифметики.

a:=Dom::Quaternion([1,2,3,4]):
b:=Dom::Quaternion([11,2,33.3,2/3]):
a*b, a+b, a^2/3, b^3;

Пример 3

Больше математических операций:

a:=Dom::Quaternion([1,2,3,4]):
b:=Dom::Quaternion([11,2,33.3,2/3]):
Dom::Quaternion::nthroot(b,3);
abs(a), sign(b)

Пример 4

Некоторые разные операции.

a:=Dom::Quaternion([1,2,3,4]):
Dom::Quaternion::matrixform(a);
map(a, sqrt), map(a, _plus, 1);

Параметры

listi

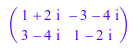
Список, содержащий четыре элемента типа Type::Real

ex

Арифметическое выражение

M

Матрица типа Dom::Matrix(Dom::Complex). Это должно иметь специальную форму, описанную в разделе Details.

Записи

"характеристика"

характеристика этой области 0

"один"

единичный элемент; это равняется Dom::Quaternion([1,0,0,0]).

размер

количеством кватернионов является infinity.

"нуль"

Нулевой элемент; это равняется Dom::Quaternion([0,0,0,0]).

Методы

развернуть все

Математические методы

_mult(x, y, …)

_plus(x, y, …)

_power(x, n)

Im(x)

Результатом является все еще кватернион.

Re(x)

Результат имеет тип Type::Real.

abs(x)

Результат имеет тип Type::Real.

conjugate(x)

intpower(x, {DOM_INT})

Реализация использует “повторенную обработку на квадрат”.

Dom::Quaternion используется "_power".

nthroot(x, n)

Реализация использует “повторенную обработку на квадрат”.

Dom::Quaternion используется "_power".

norm(x)

Результат имеет тип Type::Real.

random()

scalarmult(s, x)

scalarprod(x, y)

sign(x)

Результат имеет тип Type::Real.

Методы преобразования

convert(x)

convert_to(x, T)

Это в настоящее время обрабатывает следующие области для T: DOM_EXPR, DOM_LIST, Dom::Matrix (Dom::Complex).

expr(x)

Результатом является объект области ядра DOM_EXPR.

Этот метод перегружает функциональный expr для кватернионов, т.е. можно использовать его в форме expr(x).

matrixform(x)

Результатом является объект доменного Dom::Matrix(Dom::Complex).

Технические методы

map(x, f, arg, …)

Если дополнительные аргументы присутствуют, то каждый co компонента x заменяется f (co, аргумент...). Таким образом для кватерниона x: = a + bi + cj + dk, Dom::Quaternion(x, f, arg, ...) возвращает кватернион f (a, arg, …) + f (b, arg, …)  i + f (c, arg, …)  j + f (d, arg, …)  k.

simplify(x)

Смотрите также

Области MuPAD

Документация Symbolic Math Toolbox
Поддержка