linalg:: frobeniusFormФорма Frobenius матрицы
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
linalg::frobeniusForm(A, <All>)
linalg::frobeniusForm(A) возвращает форму Frobenius матричного A, также названного Рациональной Канонической формой A.
linalg::frobeniusForm(A, All) вычисляет форму Frobenius R A и матрицы преобразования P, таким образом что P RP-1.
Форма Frobenius, как вычислено linalg::frobeniusForm уникальна (см. ниже).
Звонок компонента A должен быть полем, т.е. областью категории Cat::Field.
Форма Frobenius следующей матрицы по ℂ:
A := Dom::Matrix(Dom::Complex)( [[1, 2, 3], [4, 5, 6], [7, 8, 9]] )

матрица:
R := linalg::frobeniusForm(A)

P матрицы преобразования может быть выбран из списка [R, P], который является результатом linalg::frobeniusForm с опцией All:
P := linalg::frobeniusForm(A, All)[2]

Мы проверяем результат:
P * R * P^(-1)

|
Квадратная матрица области категории |
|
Возвращает список |
Матрица того же доменного типа как A или список [R, P], когда опция All дан.
Ссылка: П. Осельо: Calcul точный des формирует матрицу de Jordan et de Frobenius d'une, стр 30–43. Thèse de l'Universite Scientifique Technologique et Medicale de Grenoble, 1987
Форма Frobenius квадратной матрицы A является матрицей
 ,
,
где R 1, …, R r известен как сопровождающие матрицы и имеет форму:
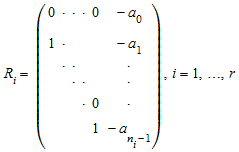 .
.
В последнем столбце сопровождающей матрицы R i вы видите коэффициенты его минимального полинома в порядке возрастания, т.е. полиномиальный m i: = X n i + a n i - 1 Xni - 1 + … + a 1 X + a 0 является минимальным полиномом матричного R i.
Для этих полиномов следующее содержит: m i + 1 делит m i для i = 1, …, r - 1, и продукт всего i m для i = 1, …, r, дает факторизацию характеристического полинома матричного A. Форма Frobenius, заданная таким образом, уникальна.