числовой::Параметры мясника схем Runge-Kutta
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
numeric::butcher(EULER1 | RKF43 | xRKF43 | RK4 | RKF34 | xRKF34 | RKF54a | xRKF54a | RKF54b | xRKF54b | DOPRI54 | xDOPRI54 | CK54 | xCK54 | RKF45a | xRKF45a | RKF45b | xRKF45b | DOPRI45 | xDOPRI45 | CK45 | xCK45 | DOPRI65 | xDOPRI65 | DOPRI56 | xDOPRI56 | BUTCHER6 | RKF87 | xRKF87 | RKF78 | xRKF78 | DOPRI87 | xDOPRI87 | DOPRI78 | xDOPRI78 | GAUSS(s) | GAUSS = s, <digits>)
numeric::butcher(method) возвращает параметры Мясника схемы Runge-Kutta под названием method.
s этапный Метод Рунге-Кутта для численного интегрирования динамической системы
с размером шага h является картой
.
“Промежуточные стадии” k 1, …, k s задан как решения алгебраических уравнений
.
Если s ×s “Матрица мясника” a ij является строго нижним треугольным, метод называется “явный”. В этом случае промежуточные стадии вычисляются рекурсивно как:
.
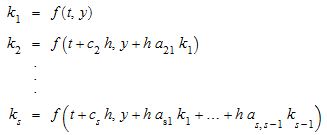Различные числовые схемы являются результатом различного выбора параметров Мясника: s ×s-matrix a ij, веса b = [b 1, …, b s] и абсциссы c = [c 1, c 2, …, c s].
Встроенные пары Методов Рунге-Кутта состоят из двух методов, которые совместно используют матричный a ij и абсциссы c i, но используют различные веса b i.
Возвращенный список [s, c, a, b1, b2, order1, order2] содержит данные Мясника метода: s является количеством этапов, c является списком абсцисс, a является матрицей Мясника, b1 и b2 являются списками весов. Целые числа order1 и order2 являются порядками схемы при использовании весов b1 или b2, соответственно, в сочетании с матричным a и абсциссами c.
Методы EULER1 (порядок 1), RK4 (порядок 4) и BUTCHER6 (порядок 6) являются отдельными методами с b1 = b2 и order1 = order2. Все другие методы являются встроенными парами Runge-Kutta-Fehlberg (RKFxx), Dormand-принц (DOPRIxx) или Наличные-деньги-Karp (CKxx) тип. Имена указывают на порядки подпроцессов, например, CK45 является Наличной-Karp парой порядков 4 и 5. CK54 является той же парой с обратным упорядоченным расположением подпроцессов. Второй подпроцесс используется, чтобы произвести временной шаг Метода Рунге-Кутта, первый подпроцесс используется для оценки ошибки временного шага.
Методы GAUSS(s) или, эквивалентно, GAUSS = s является неявными методами Гаусса с этапами s порядка 2 s.
Данные всех явных методов возвращены как точные рациональные числа. Данные методов Гаусса возвращены как числа с плавающей запятой.
Данные Мясника вызваны стандартными программами numeric::odesolve, numeric::odesolve2 и numeric::odesolveGeometric.
При вычислении данных для GAUSS(s) функция чувствительна к переменной окружения DIGITS, который определяет числовую рабочую точность.
Данные Мясника классических 4 этапов, 4-й порядок схема Runge-Kutta:
numeric::butcher(RK4)
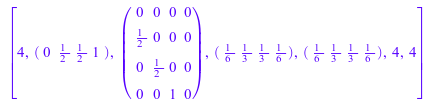
Обратите внимание на то, что веса b1 и b2 совпадают: этот классический метод не обеспечивает встроенную пару.
Данные Мясника (неявных) 3 этапов метод Гаусса:
DIGITS := 5: numeric::butcher(GAUSS(3)); delete DIGITS:
Данные Мясника встроенного парного RKF34 Runge-Kutta-Fehlberg порядков 3 и 4:
[s, c, a, b1, b2, order1, order2] := numeric::butcher(RKF34):
Количеством этапов, s 4-го подпроцесса порядка равняется 5, абсциссы c и матричный a, дают:
s, c, a
Используя эти параметры с весами
b1, b2
приводит к числовой схеме порядка 3 или 4, соответственно:
order1, order2
delete s, c, a, b1, b2, order1, order2:
Мы строим области устойчивости двух подметодов DOPRI78. Функцией устойчивости схемы Runge-Kutta с параметрами Мясника (c, a, b) дают
,
где e является вектор-столбцом (1, 1, …, 1) T. Для явного s этапная схема (матричный a является строго нижним треугольным), эта функция устойчивости уменьшает до полинома
.
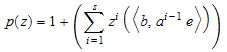Мы вычисляем коэффициенты полиномов устойчивости, сопоставленных с матрицей Мясника a и веса b1 и b2 подметодов DOPRI78:
[s, c, a, b1, b2, order1, order2] := numeric::butcher(DOPRI78):
e := matrix([1 $ s]):
a := float(matrix(a)):
b1 := linalg::transpose(float(matrix(b1))):
b2 := linalg::transpose(float(matrix(b2))):
for i from 1 to s do
c1[i] := (b1*a^(i-1)*e)[1, 1];
c2[i] := (b2*a^(i-1)*e)[1, 1];
end_for:Мы задаем полиномы устойчивости:
z := x + I*y: p1 := 1 + _plus(c1[i]*z^i $ i = 1..s): p2 := 1 + _plus(c2[i]*z^i $ i = 1..s):
Контур области устойчивости
является кривой, заданной |p (z) | = 1. Мы строим эти неявные кривые, сопоставленные с полиномами устойчивости p1(z) и p2(z), заданный выше:
plot(plot::Implicit2d(abs(p1) = 1, x = -6..1, y = 0..6,
Color = RGB::Red, Legend = "Order 7"),
plot::Implicit2d(abs(p2) = 1, x = -6..1, y = 0..6,
Color = RGB::Blue, Legend = "Order 8"),
Scaling = Constrained):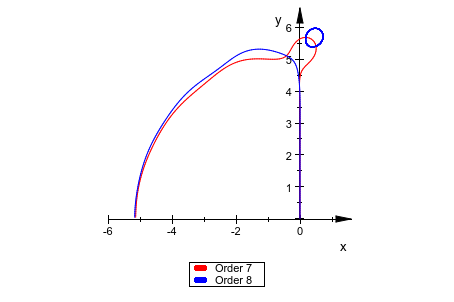
delete s, c, a, b1, b2, order1, order2, e, c1, c2, z, p1, p2:
|
Количество этапов метода Гаусса: положительное целое число |
|
Количество значительных цифр, с которыми данные Мясника методов |
Список [s, c, a, b1, b2, order1, order2] возвращен.
Дж.К. Бучер: числовой анализ Обыкновенных дифференциальных уравнений, Вайли, Чичестера (1987).
Э. Хэрер, С.П. Норсетт и G. Более бледный: решая Обыкновенные дифференциальные уравнения I, Спрингер, Берлин (1993).
Методы DOPRI87 и DOPRI78 соответствуют методу RK8(7)13M, опубликованный в:
P.J. Принц и J.R.Dormand: Старший разряд встроил формулы Рунге-Кутта, Журнал Вычислительной и Прикладной математики 7 (1), 1981.
Параметры Мясника, обеспеченные в этой исходной газете, состоят из рациональных приближений решений уравнений порядка систем Рунге-Кутта. Параметры, обеспеченные numeric::butcher, являются точными рациональными решениями уравнений порядка. Приближения, данные принцем и Dormand, совпадают с MuPAD® точные значения через 16 десятичных цифр.