числовой::Интерполяция 2-мерными сплайнами bi-cubic
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
numeric::cubicSpline2d([x0, x1, …, xn], [y0, y1, …, ym], z, <[xBC, yBC]>, <Symbolic>)
numeric::cubicSpline2d([ x0, x1, ...], [ y0, y1, ...], z) возвращает функцию сплайна bi-cubic интерполяция данных z i, j по прямоугольной mesh (x i, y j).
Вызов S := numeric::cubicSpline2d([x0, …, xn], [y0, …, yn], z, Option) приводит к кубической функции сплайна S, интерполирующий данные (x i, y j, z i, j), т.е., S (x i, y j) = z i, j для i = 0, …, n, j = 0, …, m. Функция сплайна является кусочным bi-кубическим-полиномом: на 'закрашенной фигуре'
![]() ,
,
это имеет представление
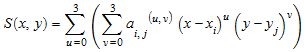
с подходящими коэффициентами a i, j (u, v) в зависимости от закрашенной фигуры. Сплайн S и его частные производные S x, S y, S xx, S xy, S yy, S xxy, S xyy, S xxyy является непрерывными функциями по целому x, плоскости y. В x - направление, S расширяет полиномиальное представление на граничных закрашенных фигурах![]() и
и![]() к
к![]() и
и![]() , соответственно. То же самое содержит относительно y - направление.
, соответственно. То же самое содержит относительно y - направление.
По умолчанию граничные условия NotAKnot приняты, т.е. частные производные S xxx, S yyy, …, S xxxyyy, непрерывен в точках с x - координирует x 1 и x, n - 1 или y - координирует y 1 и y m - 1.
По умолчанию все входные данные преобразованы в числа с плавающей запятой. Это преобразование может быть подавлено опцией Symbolic.
Без опции Symbolic, абсциссы x i, y j должен быть числовыми действительными значениями в порядке возрастания. Если эти данные не упорядочены, то numeric::cubicSpline2d переупорядочивает абсциссы внутренне, выдавая предупреждение.
Функциональный S, возвращенный numeric::cubicSpline2d, может быть вызван два, три, четыре, или пять аргументов, соответственно:
S(x, y) вызова возвращает арифметическое выражение, если x и y являются числовыми выражениями. Плавание возвращено, если или x или y являются плаванием, и все включенные параметры могут быть преобразованы в плавания.
Если или x или y содержат символьные объекты, символьный вызов, S(x, y) возвращен.
Вызов S(x, y, [u, v]) с неотрицательными целыми числами u, v возвращает частную производную![]() сплайна. Если или x или y содержат символьные объекты, символьный вызов
сплайна. Если или x или y содержат символьные объекты, символьный вызов, S(x, y, [u, v]) возвращен. Результат 0 если любой u> 3 или v> 3. Вызовы S(x, y, [0, 0]) и S(x, y) эквивалентны.
Вызов S(x, y, i, j) с неотрицательными целыми числами i, j возвращает полиномиальное представление сплайна на закрашенной фигуре p i, j. Здесь, x и y могут быть произвольными числовыми или символьными арифметическими выражениями. Внутренне, (x, y) приняты, чтобы лечь в закрашенной фигуре p i, j.
Вызов S(x, y, i, j, [u, v]) с неотрицательными целыми числами i, j, u, v возвращает полиномиальное представление частных производных функции сплайна. В этом вызове x и y могут быть произвольными числовыми или символьными арифметическими выражениями, которые приняты, чтобы лечь в закрашенной фигуре p i, j. Результат 0 если любой u> 3 или v> 3. Вызовы S(x, y, i, j, [0, 0]) и S(x, y, i, j) эквивалентны.
Если S сгенерирован с символьными абсциссами x i, y j (обязательно использующий опцию Symbolic), вызов, S(x, y, [ u , v ]) возвращен символически. Вызов S(x, y, i, j, [ u , v ]) должен использоваться для символьных абсцисс!
Мы демонстрируем некоторые вызовы с числовыми входными данными. Функциональный f (x, y) = sin (2 π (x + y)) с 0 ≤ x ≤ 1, 0 ≤ y ≤ 1 должен быть интерполирован n + 1 = 11 равноотстоящих точек в x - направление и m + 1 = 13 равноотстоящих точек в y - направление:
f := (x, y) -> sin((x + y)*2*PI): n := 10: x := [i/n $ i = 0..n]: m := 12: y := [j/m $ j = 0..m]: z := array(0..n, 0..m, [[f(i/n, j/m) $ j = 0..m] $ i = 0..n]): S1 := numeric::cubicSpline2d(x, y, z, [NotAKnot, NotAKnot]): S2 := numeric::cubicSpline2d(x, y, z, [Natural, Natural]): S3 := numeric::cubicSpline2d(x, y, z, [NotAKnot, Periodic]):
Мы рассматриваем граничные условия Complete в y - направление. Они состоят из значений f y (x i, y 0) = f y (x i, 0) = 2 π cos (2 π x i) и f y (x i, y m) = f y (x i, 1) = 2 π cos (2 π x i):
ybc:= [[2*PI*cos(2*PI*i/n) $ i = 0..n],
[2*PI*cos(2*PI*i/n) $ i = 0..n]]:
S4 := numeric::cubicSpline2d(x, y, z, [Periodic, Complete = ybc]):В точках mesh (x i, y j), входные данные z i, воспроизводится j:
x := 4/n: y := 8/m: float(f(x, y)), S1(x, y), S2(x, y), S3(x, y), S4(x, y)
![]()
Интерполяция между точками mesh зависит от граничного условия:
x := 0.92: y:= 0.55: S1(x, y), S2(x, y), S3(x, y), S4(x, y)
![]()
Приближение значения функции f (0.92, 0.55) хорош для NotAKnot, Periodic и граничных условий Complete. Граничные условия Natural являются менее соответствующими, потому что вторые частные производные функционального f не исчезают на контурах. Следовательно, ошибка приближения S2 больше, чем другие ошибки приближения:
z := float(f(x, y)): S1(x, y) - z, S2(x, y) - z, S3(x, y) - z, S4(x, y) - z
![]()
Это - bi-кубический-полином в X, Y, задающий сплайн S1 на закрашенной фигуре![]()
![]() :
:
expand(S1(X, Y, 0, 3))

delete f, n, m, ybc, x, y, z, S1, S2, S3, S4:
Мы демонстрируем некоторые вызовы с символьными данными. С опцией Symbolic используется точная арифметика:
S := numeric::cubicSpline2d(
[i $ i = 0..3],
[j $ j = 0..4],
array(0..3, 0..4, [[z.i.j $ j = 0..4] $ i = 0..3]),
Symbolic
):S(1/2, 3/2)

Это - bi-кубический-полином в X, Y, задающий сплайн с x 0 = 0 ≤ X ≤ x 1 = 1, y 1 = 1 ≤ Y ≤ y 2 = 2:
expand(S(X, Y, 0, 1))
![]()
delete S:
Мы рассматриваем интерполяцию сплайна функции![]() с - 1 ≤ x ≤ 1, - 1 ≤ y ≤ 1:
с - 1 ≤ x ≤ 1, - 1 ≤ y ≤ 1:
n := 10: xmesh := [-1 + 2*i/n $ i = 0..n]:
m := 12: ymesh := [-1 + 2*j/n $ j = 0..m]:
f := (x, y) -> exp(-x^2 - y^2):
z := array(0..n, 0..m,
[[f(-1 + 2*i/n, -1 + 2*j/m) $ j=0..m] $ i = 0..n]):
S := numeric::cubicSpline2d(xmesh, ymesh, z):Мы строим функцию сплайна S (x, y):
plotfunc3d(S(x, y), x = -1 .. 1, y = -1 .. 1):
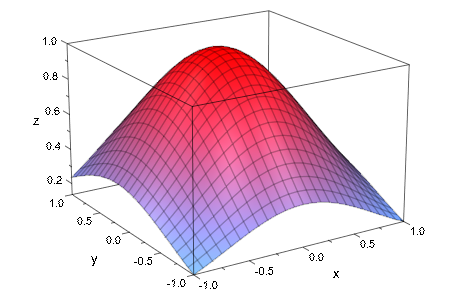
Мы строим частную производную S xxxyyy (x, y). Это постоянно на каждой закрашенной фигуре с, схватил контуры закрашенных фигур. Использование средства отображения [5 n + 1, 5 m + 1] поймало в сети точки: в каждом направлении 4 дополнительных очка между смежными точками mesh сплайна используются для графического представления:
plotfunc3d(S(x, y, [3, 3])/10, x = -1 .. 1, y = -1 .. 1,
Mesh = [5*n + 1, 5*m+ 1])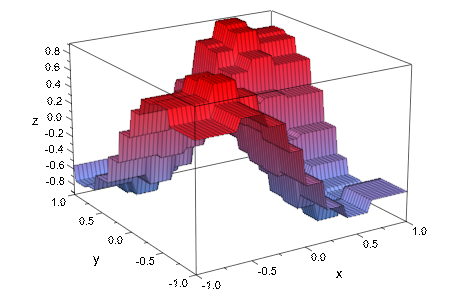
delete n, xmesh, m, ymesh, f, z, S:
Мы демонстрируем интерпретацию сплайна поверхности. Мы считаем сферу параметризованной сферическими координатами u, v с 0 ≤ u ≤ 2 π, 0 ≤ v ≤ π:
![]() .
.
Мы интерполируем функции x, y, z по прямоугольной mesh в u - v-плоскость. Начиная с x y и (trivally) z является 2 π-periodic в u, мы выбираем граничные условия Periodic для u. Для v мы выбираем граничные условия Complete с граничными значениями первого частичного v - производная, соответствующая параметризации:
x:= (u, v) -> cos(u)*sin(v): x_v := diff(x(u, v), v):
y:= (u, v) -> sin(u)*sin(v): y_v := diff(y(u, v), v):
z:= (u, v) -> cos(v): z_v := diff(z(u, v), v):
n := 4: umesh := [i*2*PI/n $ i = 0..n]:
m := 4: vmesh := [j*PI/m $ j = 0..m]:
vBC := Complete = [
[subs(x_v, u = umesh[i], v = vmesh[1]) $ i = 1 .. n+1],
[subs(x_v, u = umesh[i], v = vmesh[n + 1]) $ i = 1 .. n+1]]:
X := numeric::cubicSpline2d(umesh, vmesh,
array(0..n, 0..m, [[x(i*2*PI/n, j*PI/m) $ j=0..m] $ i=0..n]),
[Periodic, vBC]):
vBC := Complete = [
[subs(y_v, u = umesh[i], v = vmesh[1]) $ i = 1 .. n+1],
[subs(y_v, u = umesh[i], v = vmesh[n + 1]) $ i = 1 .. n+1]]:
Y := numeric::cubicSpline2d(umesh, vmesh,
array(0..n, 0..m, [[y(i*2*PI/n, j*PI/m) $ j=0..m] $ i=0..n]),
[Periodic, vBC]):
vBC := Complete = [
[subs(z_v, u = umesh[i], v = vmesh[1]) $ i = 1 .. n+1],
[subs(z_v, u = umesh[i], v = vmesh[n + 1]) $ i = 1 .. n+1]]:
Z := numeric::cubicSpline2d(umesh, vmesh,
array(0..n, 0..m, [[z(i*2*PI/n, j*PI/m) $ j=0..m] $ i=0..n]),
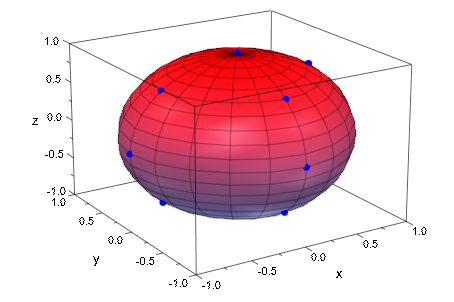
[Periodic, vBC]):С только (n + 1) × (m + 1) = 5×5 точки mesh, поверхность сплайна приводит к значительному приближению сферы. Узлы интерполяции добавляются к графику как синие точки:
plot(
plot::Surface([X(u, v), Y(u, v), Z(u, v)],
u = 0..2*PI, v = 0..PI,
Mesh = [5*n + 1, 5*m + 1],
Color = RGB::Red),
plot::Point3d(x(umesh[i], vmesh[j]),
y(umesh[i], vmesh[j]),
z(umesh[i], vmesh[j]),
PointSize = 2*unit::mm,
Color = RGB::Blue
) $ i = 1..n+1 $ j = 1..m+1
):
delete x, x_v, y, y_v, z, z_v, n, m,
umesh, vmesh, vBC, X, Y, Z:
|
x - координаты узлов: отличные числовые действительные значения в порядке возрастания |
|
y - координаты узлов: отличные числовые действительные значения в порядке возрастания |
|
Значения функции: массив формы |
|
Тип граничного условия: граничное условие в x - или y - направление может быть одним из флагов Граничные условия В y - направление, которое они оценивают, может быть передано в форме |
|
При использовании этой опции не происходит никакое преобразование входных данных к числам с плавающей точкой. Символьные абсциссы x i, y j приняты. Упорядоченное расположение x 0 <x 1 <… <x n, y 0 <y 1 <… <y m принят. Это упорядоченное расположение не проверяется, даже если координаты узла числовые! |
|
С граничным условием по умолчанию Это граничное условие рекомендуется, если никакая информация о поведении данных около контуров mesh не доступна. |
|
Граничное условие Это граничное условие рекомендуется, если известно, что данные соответствуют поверхности с исчезающим искривлением около контуров mesh. |
|
Граничное условие
Или
Соответственно. При использовании этой опции, входные данные z 0, j, z n, j, соответственно z i, 0, z должен совпасть i, m. В противном случае ошибка повышена. Это граничное условие рекомендуется, если интерполяция должна представлять периодическую функцию. |
|
Опция, заданная как Граничное условие Граничное условие Символьные данные a k, b k принят. Это граничное условие рекомендуется если данные z i, j correpond к функции с известными значениями первых частных производных на контурах mesh. |
Функция сплайна: процедура MuPAD®.