Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
Когда вычислительные собственные значения и собственные вектора некоторых матриц символически, можно получить длинный результат в форме, которая не подходит для дальнейших вычислений. Например, функция linalg::eigenvectors возвращает следующие результаты для собственных значений и собственных векторов 3 ×3 Гильбертовых матриц:
H := linalg::hilbert(3): eigen := linalg::eigenvectors(H)
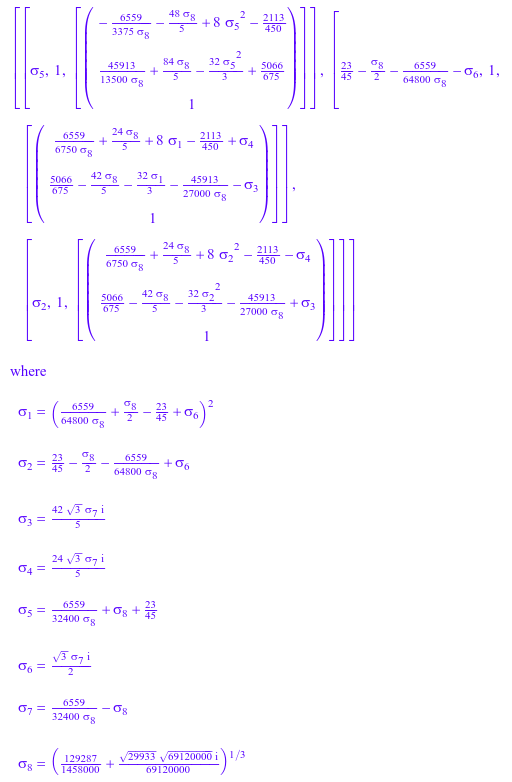
Числовое приближение результата, возвращенного символьной функцией linalg::eigenvectors, дает более короткий ответ, который содержит комплексные числа:
float(eigen)

Если вам нужно простой (хотя аппроксимированный) собственные значения и собственные вектора Гильбертовой матрицы в дальнейших вычислениях, используйте числовые методы с начала. Чтобы аппроксимировать собственные значения и собственные вектора матрицы численно, используйте функцию numeric::eigenvectors. Функция возвращает собственные значения, собственные вектора и остатки (оцененные ошибки для числовых собственных значений):
[eigenvalues, eigenvectors, residues] := numeric::eigenvectors(H)

Маленькие значения остатка указывают, что ошибки округления не значительно влияют на результаты. Чтобы подавить вычисление остатков, используйте опцию NoResidues:
numeric::eigenvectors(H, NoResidues)

Если вы хотите вычислить только собственные значения матрицы, используйте функцию numeric::eigenvalues:
numeric::eigenvalues(H)
![]()
Когда вычислительные собственные значения и собственные вектора численно, можно использовать HardwareFloats, и опции SoftwareFloats, чтобы использовать оборудование или программное обеспечение пускают в ход арифметику, соответственно. Для получения информации об этих опциях смотрите раздел Numeric Determinant. Для получения дополнительной информации смотрите страницы справки numeric::eigenvalues и numeric::eigenvectors.