Документация

Дискретные преобразования Фурье

Дискретное преобразование Фурье (DFT) является эквивалентом преобразования Фурье для дискретных данных. Одномерное дискретное преобразование Фурье элементов данных N L = [L ₁, …, L _N] задано как список F = [F ₁, …, F _N], такой что

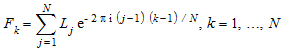Обратное дискретное преобразование Фурье задано как список L следующих элементов:

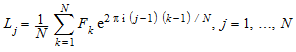MuPAD^® использует алгоритм быстрого преобразования Фурье (FFT), чтобы вычислить дискретное и обратные дискретные преобразования Фурье. Для любого N вычислительными затратами является O (N  log₂ (N)). Чтобы вычислить дискретные преобразования Фурье, используйте следующие функции:

Эти функции принимают списки (область вводят DOM_LIST), массивы (область вводят DOM_ARRAY), оборудование массивы с плавающей точкой (область вводят DOM_HFARRAY), и матрицы (категория Cat::Matrix). Принятые структуры данных (за исключением списков) могут быть одной - или многомерный. Можно использовать произвольные арифметические выражения в качестве записей.

Дискретное преобразование Фурье часто используется в обработке сигналов. Это позволяет вам разлагать сигнал на набор периодических сигналов с различными частотами и анализировать те частоты. Предположим, у вас есть дискретное множество значений сигнала, выбранного по фиксированной процентной ставке. Сила сигнала быть периодической, но шум эффективно скрывает период. Например, следующий список data представляет такой сигнал:

f1 := 150: f2 := 300:
data := [sin(f1*2*PI*t/1000) + sin(f2*2*PI*t/1000)
         + 10*(frandom() - 1/2) $t = 0..1000]:

Когда вы отображаете данные на графике, сигнал кажется случайным. Шум эффективно скрывает две основных частоты сигнала:

plot(plot::Listplot(data, t = 0..1000),
		AxesTitles = ["Time", "Amplitude"],
		YAxisTitleOrientation = Vertical,
		XAxisTitleAlignment = Center, YAxisTitleAlignment = Center)

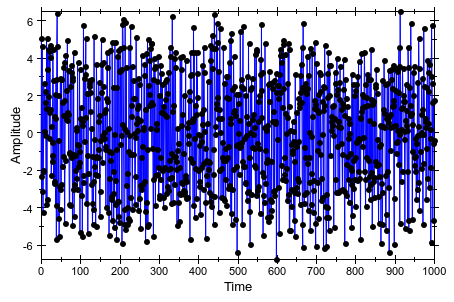
Чтобы доказать, что сигнал имеет сильный периодический компонент и найти основные частоты, вычислите дискретное преобразование Фурье сигнала:

fft := abs(numeric::fft(data)):

График fft показывает четыре peaks. Peaks соответствует двум основным частотам исходного сигнала (f1 = 150 и f2 = 300):

plot(plot::Listplot(fft, f = 0..1000),
	AxesTitles = ["Frequency", "Power"],
	YAxisTitleOrientation = Vertical,
	XAxisTitleAlignment = Center, YAxisTitleAlignment = Center)

numeric::fft и функции numeric::invfft принимают опции. Используйте опцию Symbolic, чтобы предотвратить преобразование ваших данных к числам с плавающей запятой. Например, создайте список следующих точных значений:

exactData := [sin(1/3*2*PI*n/10) $n = 0..3]

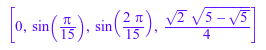
Вычислите дискретное преобразование Фурье, сохраняющее данные в его точной символьной форме:

fft := numeric::fft(exactData, Symbolic)

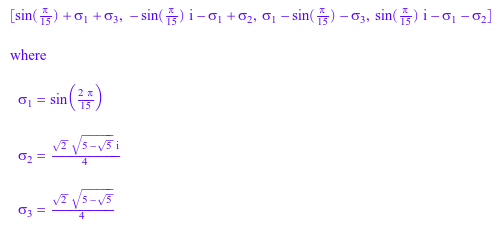
Вычислите обратное дискретное преобразование Фурье получившегося списка. Используйте функцию numeric::invfft с Symbolic, чтобы предотвратить данные от преобразования до значений с плавающей точкой:

numeric::invfft(fft, Symbolic)

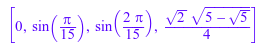
Кроме того, можно убрать результаты путем удаления очень маленьких условий. Чтобы отбросить все записи результата с абсолютными значениями, меньшими, чем времена максимальное абсолютное значение всех операндов результата, используйте опцию Clean. Эта опция также удаляет крошечные мнимые условия, которые часто появляются в результате эффектов округления. Например, без опции Symbolic, обратное преобразование Фурье от предыдущего примера возвращает следующий список значений с плавающей точкой:

numeric::invfft(fft)

Когда вы используете опцию Clean, функция numeric::invfft отбрасывает маленькие условия, которые появляются во вторых и четвертых записях получившегося списка:

numeric::invfft(fft, Clean)