Документация

Найдите Жорданову каноническую форму матрицы

Жорданова каноническая форма квадратной матрицы является блочной матрицей, в которой каждый блок является Иорданским блоком. Иорданский блок является квадратной матрицей с собственным значением исходной матрицы на основной диагонали. Блок также может содержать 1 с на своей первой супердиагонали. Каждый Иорданский блок соответствует конкретному собственному значению. Одно собственные значения производят 1×1 Иорданские блоки. Если n ×n квадратная матрица имеет n линейно независимые собственные вектора, Жорданова форма той матрицы является диагональной матрицей с собственными значениями на основной диагонали. Например, создайте 3 ×3 матрицы Паскаля P:

P := linalg::pascal(3)

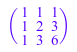
Жорданова каноническая форма матричного P является диагональной матрицей с собственными значениями на ее основной диагонали:

linalg::eigenvalues(P);
linalg::jordanForm(P)

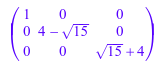
Чтобы найти Жорданову каноническую форму матрицы наряду с несингулярной матрицей преобразования подобия, T, который преобразовывает исходную матрицу к ее Жордановой форме, использует опцию All:

[J, T] := linalg::jordanForm(P, All)

Можно восстановить исходную матрицу от ее Жордановой формы и преобразования подобия:

simplify(T*J*T^(-1))

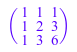
Вы не можете преобразовать к диагональной форме матрицы, для которых количество линейно независимых собственных векторов является меньше, чем матричные размерности. Например, следующая матрица имеет тройное собственное значение 2. Иорданский блок, соответствующий тому собственному значению, имеет 1 с на своей первой супердиагонали:

A := matrix([[-6, 11, -15, -11], [11, -14, 22, 16],
               [-6, 7, -7, -7], [24, -32, 43, 34]]):
linalg::jordanForm(A)

4×4 матричный A имеет тройное собственное значение 2 и только два собственных вектора:

linalg::eigenvectors(A)