Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
Аффинные линейные преобразования
с векторным b и матричным A могут быть применены к графическим объектам через объекты преобразования. Существуют специальные преобразования, такие как переводы, масштабирование, и вращения, а также общие аффинные линейные преобразования:
plot::Translate2d([b1, b2], Primitive1, Primitive2, ...) применяет перевод
векторным b = [b1, b2] ко всем точкам 2D примитивов.
plot::Translate3d([b1, b2, b3], Primitive1, ...) применяет перевод
векторным b = [b1, b2, b3] ко всем точкам 3D примитивов.
plot::Reflect2d([x1, y1], [x2, y2], Primitive1, ...) отражает все 2D примитивы о строке через точки [x1, y1] и [x2, y2].
plot::Reflect3d([x, y, z], [nx, ny, nz], Primitive1, ...) отражает все 3D примитивы о плоскости через точку [x, y, z] с нормальным [nx, ny, nz].
plot::Rotate2d(angle, [c1, c2], Primitive1, ...) вращает все точки 2D примитивов против часовой стрелки данным углом о точке опоры [c1, c2].
plot::Rotate3d(angle, [c1, c2, c3], [d1, d2, d3], Primitive1, ...) вращает все точки 3D примитивов данным углом вокруг оси вращения, заданной точкой опоры [c1, c2, c3] и направление [d1, d2, d3].
plot::Scale2d([s1, s2], Primitive1, ...) применяет диагональный масштабирующийся матричный diag (s1, s2) ко всем точкам 2D примитивов.
plot::Scale3d([s1, s2, s3], Primitive1, ...) применяет диагональный масштабирующийся матричный diag (s1, s2, s3) ко всем точкам 3D примитивов.
plot::Transform2d([b1, b2], A, Primitive1, ...) применяет общее аффинное линейное преобразование
с 2×2 матричный A и векторный b = [b1, b2] ко всем точкам 2D примитивов.
plot::Transform3d([b1, b2, b3], A, Primitive1, ...) применяет общее аффинное линейное преобразование
с 3×3 матричный A и векторный b = [b1, b2, b3] ко всем точкам 3D примитивов.
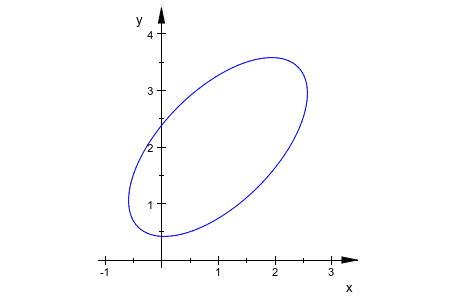
Замещающие знаки plot::Ellipse2d, обеспеченный библиотекой plot, имеют оси, параллельные осям координат. Мы используем вращение, чтобы создать эллипс с различной ориентацией:
center := [1, 2]: ellipse := plot::Ellipse2d(2, 1, center): plot(plot::Rotate2d(PI/4, center, ellipse))
Преобразуйте объекты, может быть анимирован. Мы создаем группу, состоящую из эллипса и его осей симметрии. Анимированное вращение применяется к группе:
g := plot::Group2d(
ellipse,
plot::Line2d(center, [center[1] + 2, center[2]]),
plot::Line2d(center, [center[1] - 2, center[2]]),
plot::Line2d(center, [center[1], center[2] + 1]),
plot::Line2d(center, [center[1], center[2] - 1])
):
plot(plot::Rotate2d(a, center, a = 0..2*PI, g)):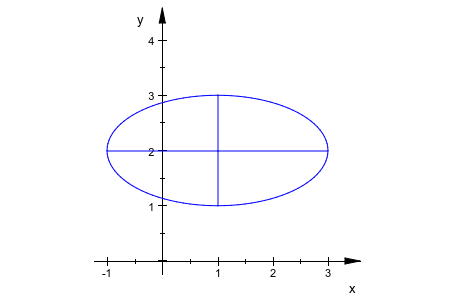
Объекты в анимированном преобразовании могут быть анимированы, также. Анимации, запущенные независимо и, могут синхронизироваться через подходящие значения TimeRange, как описано в разделе Advanced Animations: Модель Синхронизации.
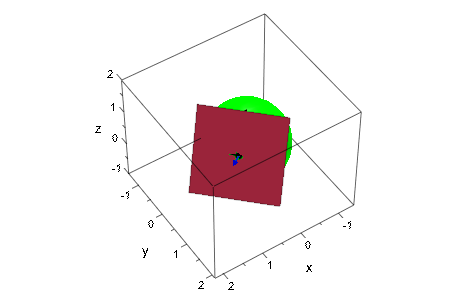
Мы генерируем сферу s радиуса r с центром c = (c x, c y, c z). Мы хотим визуализировать плоскость касательной в различных точках поверхности. Мы запускаем с плоскости касательной Северного полюса и вращаем его вокруг осей y (т.е. вдоль строки с нулевой долготой) углом в полярных координатах θ в течение первых 3 секунд. Затем это вращается вокруг z - ось (т.е. вдоль строки с постоянной широтой) углом азимута ϕ. Мы заканчиваем с плоскостью касательной в точке x = c x + cos (ϕ) sin (θ), y = c y + sin (ϕ) sin (θ), z = c z + cos (θ). Эти два вращения поняты как вложенная анимация: Путем определения непересекающихся областей значений времени запускается второе вращение (вокруг z - ось), когда первое вращение (вокруг y - ось) закончено:
r := 1: // the radius of the sphere
R := 1.01: // increase the radius a little bit
c := [0, 0, 0]: // the center of the sphere
thet := PI/3: // spherical coordinates of
phi := PI/4: // the final point p
// the final point:
p := plot::Point3d(c[1] + R*cos(phi)*sin(thet),
c[2] + R*sin(phi)*sin(thet),
c[3] + R*cos(thet),
PointSize = 2*unit::mm,
Color = RGB::Black):
// the sphere:
s := plot::Sphere(r, c, Color = RGB::Green):
// the meridian at thet = 0
c1 := plot::Curve3d([c[1] + R*sin(t), c[2], c[3] + R*cos(t)],
t = 0..thet, Color = RGB::Black):
// the meridian at thet = 0
c2 := plot::Curve3d([c[1] + R*cos(t)*sin(thet),
c[2] + R*sin(t)*sin(thet),
c[3] + R*cos(thet)],
t = 0..phi, Color = RGB::Black):
// form a group consisting of the tangent plane and its normal:
g := plot::Group3d(
plot::Surface([c[1] + u, c[2] + v, c[3] + R],
u = -1..1, v = -1..1,
Mesh = [2, 2], Color = RGB::Red.[0.3]),
plot::Arrow3d([c[1], c[2], c[3] + R],
[c[1], c[2], c[3] + R + 0.7])
):
// rotate the group for 3 seconds along the meridian:
g := plot::Rotate3d(a, c, [0, 1, 0], a = 0..thet,
g, TimeRange = 0..3):
// rotate the group for further 3 seconds along the azimuth:
g := plot::Rotate3d(a, c, [0, 0, 1], a = 0..phi,
g, TimeRange = 3..6):
plot(s, g, c1, c2, p, CameraDirection = [2, 3, 4]):