Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
Упрощение математического выражения не является ясно заданным предметом. Нет никакой универсальной идеи, относительно которой форма выражения является самой простой. Форма математического выражения, которое является самым простым для одной проблемы, оказывается сложной или даже неподходящей для другой проблемы. Например, следующие два математических выражения представляют тот же полином в различных формах:
(x + 1) (x - 2) (x + 3) (x - 4),
x 4 - 2 x3 - 13 x2 + 14 x + 24.
Первая форма ясно показывает корни этого полинома. Эта форма более проста для работы с корнями. Вторая форма служит лучше всего когда это необходимо коэффициентам полинома.
Если проблема, которую вы хотите решить, требует конкретной формы выражения, лучший подход должен выбрать соответствующую функцию упрощения. Смотрите Функции Упрощения Выбора.
Помимо определенного simplifiers, MuPAD® предлагает два общих единиц:
simplify ищет более простую форму путем перезаписи условий выражения. Эта функция использует внутренний ряд правил для перезаписи выражения. Вы не можете изменить этот ряд правил.
Simplify выполняет более обширный поиск простой формы выражения. Для некоторых выражений эта функция может быть медленнее, но более гибкой и более мощной, чем simplify. Simplify использует более широкий ряд правил, чтобы искать более простую форму выражения. Simplify позволяет вам расширить набор правил упрощения и также принимает много опций, разрешающих вам больше управления алгоритмом упрощения.
Если вам не нужна конкретная форма выражений (расширенный, учтенный, или выразил в конкретных терминах), используйте simplify и Simplify, чтобы сократить математические выражения. Например, используйте эти функции, чтобы найти более короткую форму для конечного результата. Общий simplifiers также может помочь вам в проверке результата.
Используйте команду simplify, чтобы упростить элементарные выражения, такие как:
simplify((x - 1)*(x + 1)*(x^2 + x + 1)*(x^2 + 1)* (x^2 - x + 1)*(x^4 - x^2 + 1)); simplify(cos(x)^(-2) - tan(x)^2)
![]()
![]()
Для элементарных выражений simplify является эффективным и быстрым simplifier. Для более сложных выражений simplify может быть менее эффективным. Возвращенная форма следующего выражения может быть сокращена далее. Simplify возвращает более простую форму:
f := (cos(x)^2 - sin(x)^2)/(sin(x)*cos(x)): simplify(f), Simplify(f)

По умолчанию, в порядке найти самую простую форму выражения, функция Simplify делает один шаг упрощения. Эта функция может упростить некоторые выражения далее путем делания большего количества шагов упрощений:
F := exp((cos(x)^2 - sin(x)^2)*sin(2*x)*(exp(2*x)
-2*exp(x) + 1)/(exp(2*x) - 1)):
Simplify(F)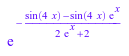
Можно изменить количество внутренних шагов упрощения через опцию Steps. Эта опция не доступна для simplify:
Simplify(F, Steps = 250)

По умолчанию общие simplifiers возвращают только одну форму выражения — форма, которую MuPAD считает самым простым. Чтобы возвратить все формы, найденные Simplify, используйте опцию All:
Simplify((x - 1)*(x + 1)*(x^2 + x + 1)*(x^2 + 1)
*(x^2 - x + 1)*(x^4 - x^2 + 1), All)
При преобразовании выражения MuPAD simplifiers сохраняет все формы выражения математически эквивалентными начальному выражению. Например, simplifiers не комбинируют логарифмы. Правило для объединения логарифмов не содержит для произвольных сложных аргументов и, поэтому, комбинирование логарифмов может быть неправильным для некоторых параметров:
Simplify(ln(x + 2) - ln(x^2 + 4*x + 4))
![]()
Потенциальное деление на нуль является единственным исключением из этого правила:
Simplify(x*(x + 1)/x)
![]()
Чтобы применить больше правил упрощения, которые не обычно правильны, но которые могут возвратить более простые результаты, используйте опцию IgnoreAnalyticConstraints. Эта опция доступна и для simplify и для Simplify. Например, упрощая выражение с IgnoreAnalyticConstraints, вы получаете результат с объединенными логарифмами:
Simplify(ln(x + 2) - ln(x^2 + 4*x + 4), IgnoreAnalyticConstraints)
![]()
Для списка всех опций, доступных для общего simplifiers, смотрите simplify и Simplify.