Exponenta Banner

pat2cwav

Создайте вейвлет из шаблона

Синтаксис

[PSI,XVAL,NC] = pat2cwav(YPAT,METHOD,POLDEGREE,REGULARITY)

Описание

[PSI,XVAL,NC] = pat2cwav(YPAT,METHOD,POLDEGREE,REGULARITY) вычисляет допустимый вейвлет для CWT (данный XVAL и PSI) адаптированный к шаблону, заданному векторным YPAT, и нормы, равной 1.

Базовый шаблон x-значений установлен в

xpat = linspace(0,1,length(YPAT))

Постоянный NC таков, что NC *PSI аппроксимирует YPAT на интервале [0,1] использованием выравнивания методом наименьших квадратов

  • полином степени POLDEGREE, когда METHOD равен 'polynomial'

  • проекция на пробеле функций, ортогональных к константам, когда METHOD равен 'orthconst'

Параметр REGULARITY задает граничные ограничения в точках 0 и 1. Допустимыми значениями является 'continuous', 'differentiable' и 'none'.

Когда METHOD равен 'polynomial'

  • если REGULARITY равен 'continuous', POLDEGREE должен быть больше, чем или равным 3.

  • если REGULARITY равен 'differentiable', POLDEGREE должен быть больше, чем или равным 5.

Примеры

Принцип для разработки нового вейвлета для CWT должен аппроксимировать данный шаблон с помощью оптимизации наименьших квадратов при ограничительном продвижении к допустимому вейвлету, которому хорошо удовлетворяют для обнаружения шаблона с помощью непрерывного вейвлета, преобразовывают (см. Misiti и др.).

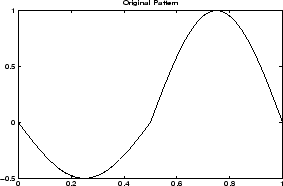
load ptpssin1; 
plot(X,Y), title('Original Pattern')


[psi,xval,nc] = pat2cwav(Y, 'polynomial',6, 'continuous') ;
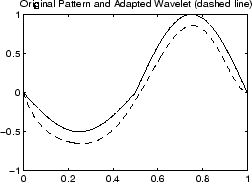
plot(X,Y,'-',xval,nc*psi,'--'), 
title('Original Pattern and Adapted Wavelet (dashed line)')

Можно проверять, что psi удовлетворяет определение вейвлета путем отмечания, что это объединяется, чтобы обнулить и что его норма L2 равна 1.

dx = xval(2)-xval(1);
Mu = sum(psi*dx)
L2norm = sum(abs(psi).^2*dx)

Ссылки

Мизити, M., И. Мизити, Г. Оппенхейм, J.-M. Poggi (2003), “Приложения Les ondelettes et leurs”, Гермес.

Представлено до R2006a

Документация Wavelet Toolbox
Поддержка