graphminspantree

Найдите минимальное дерево охвата в графике

Синтаксис

[Tree, pred] = graphminspantree(G)
[Tree, pred] = graphminspantree(G, R)
[Tree, pred] = graphminspantree(..., 'Method', MethodValue, ...)
[Tree, pred] = graphminspantree(..., 'Weights', WeightsValue, ...)

Аргументы

G N на n разреженная матрица, которая представляет неориентированного графа. Ненулевые записи в матричном G представляйте веса ребер.
RСкаляр между 1 и количество узлов.

Описание

Совет

Дополнительные сведения о функциях теории графов см. в Функциях Теории графов.

[Tree, pred] = graphminspantree(G) находит нециклическое подмножество ребер, которое соединяет все узлы в неориентированном графе G и для которого минимизирована общая масса. Веса ребер являются всеми ненулевыми записями в более низком треугольнике N на n разреженной матрицы G. Выведите Tree дерево охвата, представленное разреженной матрицей. Выведите pred вектор, содержащий узлы-предшественников минимального дерева охвата (MST), с корневым узлом, обозначенным 0. Значения по умолчанию корневого узла к первому узлу в самом большом связанном компоненте. Этот расчет требует дополнительного вызова graphconncomp функция.

[Tree, pred] = graphminspantree(G, R) устанавливает корень минимального дерева охвата к узлу R.

[Treepred ] = graphminspantree (..., 'PropertyName', PropertyValue, ...) вызовы graphminspantree с дополнительными свойствами, которые используют имя свойства / пары значения свойства. Можно задать одно или несколько свойств в любом порядке. Каждый PropertyName должен быть заключен в одинарные кавычки и нечувствительный к регистру. Это имя свойства / пары значения свойства следующие:

[Tree, pred] = graphminspantree(..., 'Method', MethodValue, ...) позволяет вам указать, что алгоритм раньше находил минимальное дерево охвата (MST). Выбор:

  • 'Kruskal' — Выращивает минимальное дерево охвата (MST) одно ребро за один раз путем нахождения ребра, которое соединяет два дерева в распространяющемся лесу роста MSTs. Временной сложностью является O(E+X*log(N)), где X не количество ребер больше, чем самое длинное ребро в MST и N и E количество узлов и ребер соответственно.

  • 'Prim' — Алгоритм по умолчанию. Выращивает минимальное дерево охвата (MST) одно ребро за один раз путем добавления минимального ребра, которое соединяет узел в растущем MST с любым другим узлом. Временной сложностью является O(E*log(N)), где N и E количество узлов и ребер соответственно.

Примечание

Когда график не связан, алгоритм Прима возвращает только дерево, которое содержит R, в то время как алгоритм Краскэла возвращает MST для каждого компонента.

[Tree, pred] = graphminspantree(..., 'Weights', WeightsValue, ...) позволяет вам задать пользовательские веса для ребер. WeightsValue вектор-столбец, имеющий одну запись для каждого ненулевого значения (ребро) в матричном G. Порядок пользовательских весов в векторе должен совпадать с порядком ненулевых значений в матричном G когда это пересечено по столбцам. По умолчанию, graphminspantree получает информацию веса от ненулевых записей в матричном G.

Примеры

  1. Создайте и просмотрите неориентированного графа с 6 узлами и 11 ребрами.

    W = [.41 .29 .51 .32 .50 .45 .38 .32 .36 .29 .21];
DG = sparse([1 1 2 2 3 4 4 5 5 6 6],[2 6 3 5 4 1 6 3 4 2 5],W);

UG = tril(DG + DG')
UG =

   (2,1)       0.4100
   (4,1)       0.4500
   (6,1)       0.2900
   (3,2)       0.5100
   (5,2)       0.3200
   (6,2)       0.2900
   (4,3)       0.5000
   (5,3)       0.3200
   (5,4)       0.3600
   (6,4)       0.3800
   (6,5)       0.2100

view(biograph(UG,[],'ShowArrows','off','ShowWeights','on'))

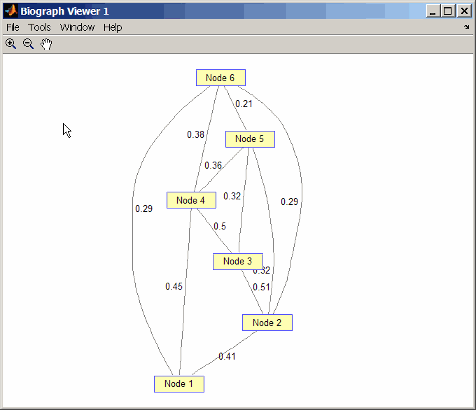
  2. Найдите и просмотрите минимальное дерево охвата неориентированного графа.

     [ST,pred] = graphminspantree(UG)

ST =

   (6,1)       0.2900
   (6,2)       0.2900
   (5,3)       0.3200
   (5,4)       0.3600
   (6,5)       0.2100


pred =

     0     6     5     5     6     1

view(biograph(ST,[],'ShowArrows','off','ShowWeights','on'))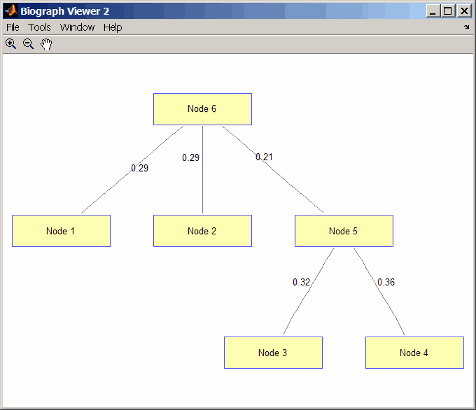

Ссылки

[1] Kruskal, J.B. (1956). На самом коротком поддереве охвата графика и проблемы коммивояжера. Продолжения американского математического общества 7, 48-50.

[2] Чопорный, R. (1957). Самые короткие сети связи и некоторые обобщения. Система Bell технический журнал 36, 1389-1401.

[3] Siek, Дж.Г. Ли, L-Q и Lumsdaine, A. (2002). Руководство пользователя библиотеки графика повышения и справочник, (верхний Сэддл-Ривер, образование НДЖ:ПИРСОНА).

Смотрите также

| | | | | | | | | |

Представленный в R2006b

Документация Bioinformatics Toolbox
Поддержка
Для просмотра документации необходимо авторизоваться на сайте