Количество циклов графа вызовов по одной или нескольким функциям
Метрика обеспечивает количественную оценку количества циклов рекурсии в вашем проекте. Метрика является суммой:
Количество прямых рекурсий (сам рекурсивные функции или функции, вызывая себя).
Количество строго связанных компонентов, сформированных косвенными циклами рекурсии в вашем проекте. Если вы рассматриваете циклы рекурсии как ориентированного графа, график строго соединяется, если существует путь между всеми парами вершин.
Вычислить количество строго связанных компонентов:
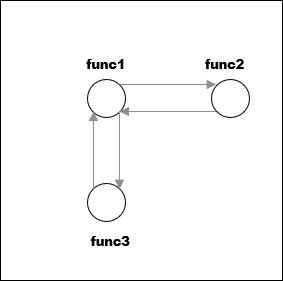
Чертите циклы рекурсии в своем коде.
Например, циклы рекурсии в этом примере показывают ниже.
volatile int checkStatus;
void func1() {
if(checkStatus) {
func2();
}
else {
func3();
}
}
func2() {
func1();
}
func3() {
func1();
}
Идентифицируйте количество строго связанных компонентов, сформированных циклами рекурсии.
В предыдущем примере существует тот, строго соединил компонент. Можно переместить от любой вершины до другой вершины следующим пути в графике.
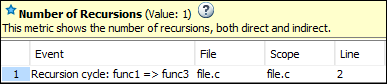
Список событий ниже метрики показывает один из циклов рекурсии в строго связанном компоненте.
Вызовы через указатель функции не рассматриваются.
Рекомендуемый верхний предел для этой метрики 0. Чтобы избежать возможности превышения доступного стекового пространства, не используйте рекурсии в своем коде. Рекурсии могут стремиться к пробелу вертикальной выхлопной трубы легко. Смотрите примеры роста размера стека с рекурсиями, описанными для этого правила CERT-C, которое запрещает рекурсии.
Чтобы обнаружить использование рекурсий, проверяйте на нарушения одного из MISRA C:2012 Rule 17.2, MISRA C®: 2 004 правила 16.2, MISRA C++:2008 Rule 7-5-4 или JSF® Rule 119. Обратите внимание на то, что эти средства проверки правила полагают, что явная функция вызывает только. Например, в Коде С++, средства проверки правила игнорируют неявные вызовы конструкторов во время создания объекта. Однако метрический расчет рассматривает и неявные и явные вызовы.
Чтобы осуществить пределы на метриках, смотрите, Вычисляют Метрики сложности кода.
int getVal(void);
void main() {
int count = getVal(), total;
assert(count > 0 && count <100);
total = sum(count);
}
int sum(int val) {
if(val<0)
return 0;
else
return (val + sum(val-1));
}В этом примере количество рекурсий равняется 1.
Прямая рекурсия является рекурсией где вызовы функции самой в ее собственном теле. Для прямых рекурсий количество рекурсий равно количеству рекурсивных функций.
volatile int signal;
void operation1() {
int stop = signal%2;
if(!stop)
operation2();
}
void operation2() {
operation1();
}
void main() {
operation1();
}В этом примере количество рекурсий является тем. Две функции operation1 и operation2 вовлечены в цикл графа вызовов operation1 → operation2 → operation1.
Косвенная функция является рекурсией где вызовы функции самой через другие функции. Для косвенных рекурсий количество рекурсий может отличаться от количества рекурсивных функций.
volatile int checkStatus;
void func1() {
if(checkStatus) {
func2();
}
else {
func3();
}
}
func2() {
func1();
}
func3() {
func1();
}В этом примере существует два цикла графа вызовов:
func1 → func2 → func1
func1 → func3 → func1
Однако циклы формируются, тот строго соединил компонент. Можно переместить от любой вершины до другой вершины следующим пути в графике. Следовательно, количество рекурсий является тем.
volatile int signal;
void operation1() {
int stop = signal%2;
if(!stop)
operation1_1();
}
void operation1_1() {
operation1();
}
void operation2() {
int stop = signal%2;
if(!stop)
operation2_1();
}
void operation2_1() {
operation2();
}
void main(){
operation1();
operation2();
}В этом примере количество рекурсий равняется двум.
Существует два цикла графа вызовов:
operation1 → operation1_1 → operation1
operation2 → operation2_1 → operation2
Циклы графа вызовов формируют два строго связанных компонента.
volatile int signal;
void operation1() {
int stop = signal%3;
if(stop==1)
operation1();
else if(stop==2)
operation2();
}
void operation2() {
operation1();
}
void main() {
operation1();
}В этом примере количество рекурсий равняется двум:
Строго связанный компонент, сформированный циклом operation1 → operation2 → operation1.
Саморекурсивная функция operation1.
| Группа: проект |
Акроним: AP_CG_CYCLE |
| Метрика HIS: да |
Calculate code metrics (-code-metrics) | MISRA C:2012 Rule 17.2