В этом примере показано, как к модели линия связи с модуляцией PSK, повышенным формированием импульса косинуса, многопутевым исчезновением и адаптивной эквализацией.
Пример настраивает три сценария эквализации и вызывает отдельный скрипт, чтобы выполнить цикл обработки многократно для каждого сценария. Каждый вызов соответствует блоку передачи. Формирование импульса и многопутевой исчезающий канал сохраняют информацию состояния от одного блока до следующего. Для визуализации удара канала, исчезающего на адаптивной сходимости эквалайзера, симуляция сбрасывает состояние эквалайзера каждый блок.
Чтобы экспериментировать с различными настройками симуляции, можно отредактировать пример. Например, можно установить ResetBeforeFiltering свойство эквалайзера возражает против 0, который заставит эквалайзер сохранять состояние от одного блока до следующего.
Симуляция 1: линейная эквализация для плоского частотой исчезновения
Симуляция 2: линейная эквализация для выборочного частотой исчезновения
Симуляция 3: эквализация обратной связи решения (DFE) для Выборочного Частотой Исчезновения
Установите параметры, связанные с блоком передачи, который состоит из трех частей: обучающая последовательность, полезная нагрузка и последовательность хвоста. Все три используют ту же схему PSK; обучение и последовательности хвоста используются в эквализации. Мы используем генератор случайных чисел по умолчанию, чтобы гарантировать воспроизводимость результатов.
Rsym = 1e6; % Symbol rate (Hz) nTrain = 100; % Number of training symbols nPayload = 400; % Number of payload symbols nTail = 20; % Number of tail symbols % Set random number generator for repeatability hStream = RandStream.create('mt19937ar', 'seed', 12345);
Сконфигурируйте Систему модуляции и демодуляции PSK objects™.
bitsPerSym = 2; % Number of bits per PSK symbol M = 2^bitsPerSym; % Modulation order hPSKMod = comm.PSKModulator(M, ... 'PhaseOffset',0, ... 'SymbolMapping','Binary'); hPSKDemod = comm.PSKDemodulator(M, ... 'PhaseOffset',0, ... 'SymbolMapping','Binary'); PSKConstellation = constellation(hPSKMod).'; % PSK constellation
Сгенерируйте последовательности хвоста и обучение.
xTrainData = randi(hStream, [0 M-1], nTrain, 1); xTailData = randi(hStream, [0 M-1], nTail, 1); xTrain = step(hPSKMod,xTrainData); xTail = step(hPSKMod,xTailData);
Сконфигурируйте повышенную передачу косинуса и получите Системные объекты фильтра. Фильтры включают повышающую дискретизацию и субдискретизацию, соответственно.
chanFilterSpan = 8; % Filter span in symbols sampPerSymChan = 4; % Samples per symbol through channels hTxFilt = comm.RaisedCosineTransmitFilter( ... 'RolloffFactor',0.25, ... 'FilterSpanInSymbols',chanFilterSpan, ... 'OutputSamplesPerSymbol',sampPerSymChan); hRxFilt = comm.RaisedCosineReceiveFilter( ... 'RolloffFactor',0.25, ... 'FilterSpanInSymbols',chanFilterSpan, ... 'InputSamplesPerSymbol',sampPerSymChan, ... 'DecimationFactor',sampPerSymChan); % Calculate the samples per symbol after the receive filter sampPerSymPostRx = sampPerSymChan/hRxFilt.DecimationFactor; % Calculate the delay in samples from both channel filters chanFilterDelay = chanFilterSpan*sampPerSymPostRx;
Сконфигурируйте Системный объект канала AWGN с NoiseMethod набор свойств к Signal to noise ratio (Es/No) и Es/No установите на 20 дБ.
hAWGNChan = comm.AWGNChannel( ... 'NoiseMethod','Signal to noise ratio (Es/No)', ... 'EsNo',20, ... 'SamplesPerSymbol',sampPerSymChan);
Начните с одно пути, плоского частотой исчезающего канала. Для этого канала получатель использует простой LMS с 1 касанием (наименьшее количество среднего квадратичного) эквалайзер, который реализует автоматическое усиление и регулировку фазы.
Скрипт commadapteqloop.m запуски многократно. Каждый запуск соответствует блоку передачи. Эквалайзер сбрасывает свое состояние, и взвесьте каждый блок передачи. Чтобы сохранить состояние от одного блока до следующего, можно установить ResetBeforeFiltering свойство эквалайзера возражает против false.
Перед первым показом, commadapteqloop.m отображает Системный объект канала Рейли и свойства объекта эквалайзера. Для каждого запуска фигура MATLAB показывает визуализацию обработки сигналов. Красные круги в графиках сигнального созвездия соответствуют ошибкам символа. В графике "Весов" синие и пурпурные линии соответствуют действительным и мнимым частям, соответственно.
simName = 'Linear equalization for frequency-flat fading'; % Used to label figure window % Configure a frequency-flat Rayleigh channel System object with the % RandomStream property set to 'mt19937ar with seed' for repeatability. hRayleighChan = comm.RayleighChannel( ... 'SampleRate',Rsym*sampPerSymChan, ... 'MaximumDopplerShift',30); % Configure an adaptive equalizer object nWeights = 1; % Single weight stepSize = 0.1; % Step size for LMS algorithm alg = lms(stepSize); % Adaptive algorithm object eqObj = lineareq(nWeights,alg,PSKConstellation); % Equalizer object % Delay in symbols from the equalizer eqDelayInSym = (eqObj.RefTap-1)/sampPerSymPostRx; % Link simulation nBlocks = 50; % Number of transmission blocks in simulation for block = 1:nBlocks commadapteqloop; end
System: comm.RayleighChannel
Properties:
SampleRate: 4000000
PathDelays: 0
AveragePathGains: 0
NormalizePathGains: true
MaximumDopplerShift: 30
DopplerSpectrum: [1x1 struct]
RandomStream: 'mt19937ar with seed'
Seed: 73
PathGainsOutputPort: false
EqType: 'Linear Equalizer'
AlgType: 'LMS'
nWeights: 1
nSampPerSym: 1
RefTap: 1
SigConst: [1.0000 + 0.0000i 0.0000 + 1.0000i -1.0000 + 0.0000i -0.0000 - 1.0000i]
StepSize: 0.1000
LeakageFactor: 1
Weights: 0
WeightInputs: 0
ResetBeforeFiltering: 1
NumSamplesProcessed: 0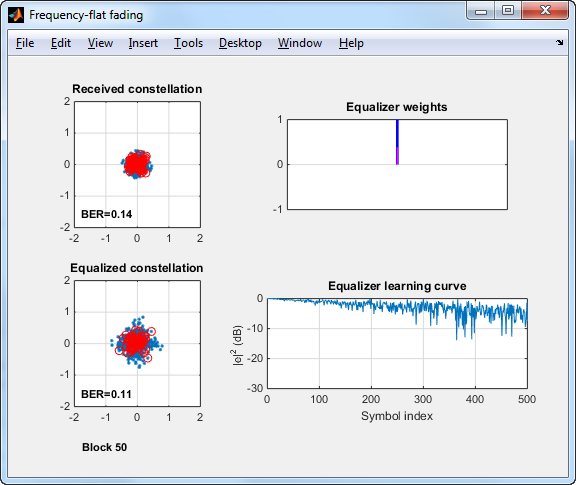
Симулируйте выборочный частотой Канал с релеевским замиранием с тремя путями. Получатель использует линейный RLS с 8 касаниями (рекурсивные наименьшие квадраты) эквалайзер с расположенными с интервалами символом касаниями.
simName = 'Linear equalization for frequency-selective fading'; % Reset transmit and receive filters reset(hTxFilt); reset(hRxFilt); % Set the Rayleigh channel System object to be frequency-selective release(hRayleighChan); hRayleighChan.PathDelays = [0 0.9 1.5]/Rsym; hRayleighChan.AveragePathGains = [0 -3 -6]; % Configure an adaptive equalizer nWeights = 8; forgetFactor = 0.99; % RLS algorithm forgetting factor alg = rls(forgetFactor); % RLS algorithm object eqObj = lineareq(nWeights,alg,PSKConstellation); eqObj.RefTap = 3; % Reference tap eqDelayInSym = (eqObj.RefTap-1)/sampPerSymPostRx; % Link simulation and store BER values BERvect = zeros(1,nBlocks); for block = 1:nBlocks commadapteqloop; BERvect(block) = BEREq; end avgBER2 = mean(BERvect)
System: comm.RayleighChannel
Properties:
SampleRate: 4000000
PathDelays: [0 9e-07 1.5e-06]
AveragePathGains: [0 -3 -6]
NormalizePathGains: true
MaximumDopplerShift: 30
DopplerSpectrum: [1x1 struct]
RandomStream: 'mt19937ar with seed'
Seed: 73
PathGainsOutputPort: false
EqType: 'Linear Equalizer'
AlgType: 'RLS'
nWeights: 8
nSampPerSym: 1
RefTap: 3
SigConst: [1.0000 + 0.0000i 0.0000 + 1.0000i -1.0000 + 0.0000i -0.0000 - 1.0000i]
ForgetFactor: 0.9900
InvCorrInit: 0.1000
InvCorrMatrix: [8x8 double]
Weights: [0 0 0 0 0 0 0 0]
WeightInputs: [0 0 0 0 0 0 0 0]
ResetBeforeFiltering: 1
NumSamplesProcessed: 0
avgBER2 =
3.0000e-04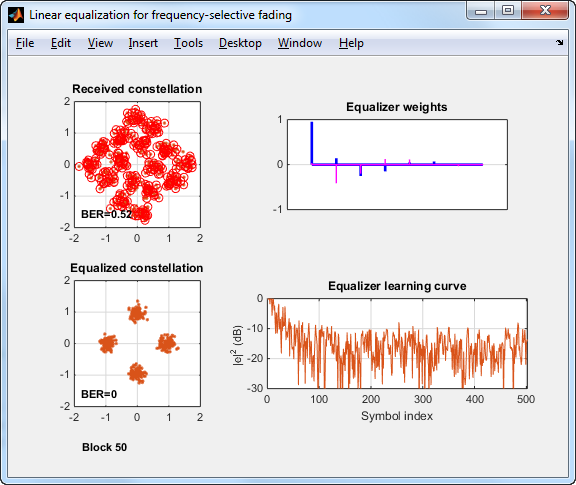
Получатель использует DFE с незначительно расположенным с интервалами прямым фильтром с шестью касаниями (две выборки на символ) и два веса обратной связи. DFE использует тот же алгоритм RLS в качестве в Симуляции 2. Получить структура фильтра восстановлена, чтобы составлять увеличенное число выборок на символ.
simName = 'Decision feedback equalization (DFE) for frequency-selective fading'; % Reset transmit filter and adjust receive filter decimation factor reset(hTxFilt); release(hRxFilt); hRxFilt.DecimationFactor = 2; sampPerSymPostRx = sampPerSymChan/hRxFilt.DecimationFactor; chanFilterDelay = chanFilterSpan*sampPerSymPostRx; % Reset fading channel reset(hRayleighChan); % Configure an adaptive equalizer object nFwdWeights = 6; % Number of feedforward equalizer weights nFbkWeights = 2; % Number of feedback filter weights eqObj = dfe(nFwdWeights, nFbkWeights,alg,PSKConstellation,sampPerSymPostRx); eqObj.RefTap = 3; eqDelayInSym = (eqObj.RefTap-1)/sampPerSymPostRx; for block = 1:nBlocks commadapteqloop; BERvect(block) = BEREq; end avgBER3 = mean(BERvect)
System: comm.RayleighChannel
Properties:
SampleRate: 4000000
PathDelays: [0 9e-07 1.5e-06]
AveragePathGains: [0 -3 -6]
NormalizePathGains: true
MaximumDopplerShift: 30
DopplerSpectrum: [1x1 struct]
RandomStream: 'mt19937ar with seed'
Seed: 73
PathGainsOutputPort: false
EqType: 'Decision Feedback Equalizer'
AlgType: 'RLS'
nWeights: [6 2]
nSampPerSym: 2
RefTap: 3
SigConst: [1.0000 + 0.0000i 0.0000 + 1.0000i -1.0000 + 0.0000i -0.0000 - 1.0000i]
ForgetFactor: 0.9900
InvCorrInit: 0.1000
InvCorrMatrix: [8x8 double]
Weights: [0 0 0 0 0 0 0 0]
WeightInputs: [0 0 0 0 0 0 0 0]
ResetBeforeFiltering: 1
NumSamplesProcessed: 0
avgBER3 =
0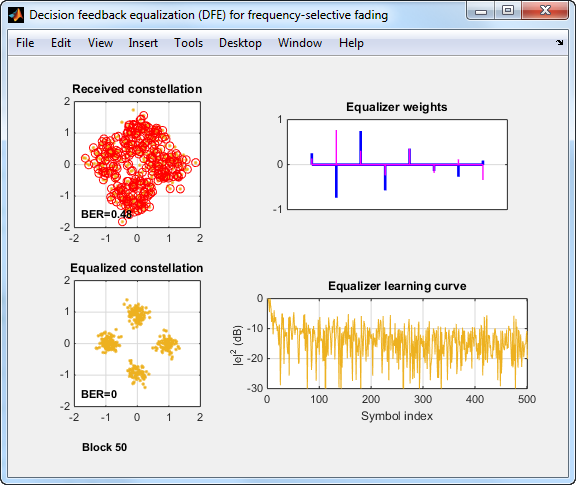
Этот пример показал относительную производительность линейных и эквалайзеров обратной связи решения и в плоских частотой и в выборочных частотой исчезающих каналах. Это показало, как эквалайзер с одним касанием достаточен компенсировать плоский частотой канал, но что выборочный частотой канал требует эквалайзера с несколькими касаниями. Наконец, это показало, что эквалайзер обратной связи решения превосходит линейный эквалайзер в выборочном частотой канале.
Этот пример использует следующий скрипт и функции помощника: