Документация

Сетевая архитектура

Обобщенная нейронная сеть регрессии (GRNN) часто используется в приближении функций. Это имеет радиальный базисный слой и специальный линейный слой.

Архитектуру для GRNN показывают ниже. Это похоже на радиальную базисную сеть, но имеет немного отличающийся второй слой.

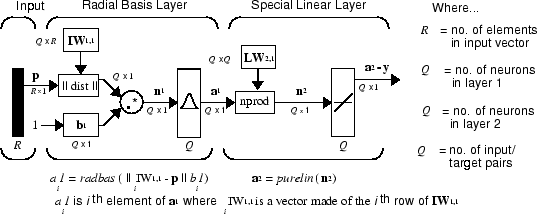
Здесь nprod поле, показанное выше (код функционируют normprod) производит S ² элемента в векторе n2. Каждый элемент является скалярным произведением строки ^LW2,1 и входного вектора a1, все нормированные суммой элементов a1. Например, предположите это

LW{2,1}= [1 -2;3 4;5 6];
a{1} = [0.7;0.3];

Затем

aout = normprod(LW{2,1},a{1})
aout =
    0.1000
    3.3000
    5.3000

Первый слой точно так же, как это для newrbe сети. Это имеет столько же нейронов, сколько там вводятся целевые векторы / в P. А именно, веса первого слоя установлены в P'. Смещение b1 установлено в вектор-столбец 0.8326/SPREAD. Пользователь выбирает SPREAD, расстояние входной вектор должно быть от вектора веса нейрона, чтобы быть 0.5.

Снова, первый слой действует точно так же, как newrbe радиальный базисный слой описан ранее. Взвешенный вход каждого нейрона является расстоянием между входным вектором и его вектором веса, вычисленным с dist. Сетевой вход каждого нейрона является продуктом своего взвешенного входа с его смещением, вычисленным с netprod. Выход каждого нейрона является своим сетевым входом, прошел через radbas. Если вектор веса нейрона будет равен (транспонированному) входному вектору, его взвешенный вход будет 0, его сетевой вход будет 0, и его выход будет 1. Если вектор веса нейрона является расстоянием spread от входного вектора его взвешенным входом будет spread, и его сетевой вход будет sqrt (−log (.5)) (или 0.8326). Поэтому его выход будет 0.5.

Второй слой также имеет столько же нейронов сколько векторы входа/цели, но здесь LW{2,1} установлен в T.

Предположим, что у вас есть входной вектор p близко к p_i, одному из входных векторов среди входного вектора / целевые пары, используемые в разработке весов слоя 1. Этот вход p производит слой 1 aⁱ выход близко к 1. Это приводит к слою 2 выход близко к t_i, одна из целей раньше формировала веса слоя 2.

Больший spread приводит к большой площади вокруг входного вектора, где нейроны слоя 1 ответят значительными выходными параметрами. Поэтому, если spread мал радиальная основная функция очень крута, так, чтобы нейрон с вектором веса, самым близким к входу, имел намного больший выход, чем другие нейроны. Сеть имеет тенденцию отвечать целевым вектором, сопоставленным с самым близким входным вектором проекта.

Как spread становится больше, наклон радиальной основной функции становится более сглаженным, и несколько нейронов могут ответить на входной вектор. Сеть затем действует, как будто она берет взвешенное среднее между целевыми векторами, входные векторы проекта которых являются самыми близкими к новому входному вектору. Как spread становится больше, все больше нейронов способствует среднему значению, так что в итоге сетевая функция становится более сглаженной.

Спроектируйте (newgrnn)

Можно использовать функциональный newgrnn создать GRNN. Например, предположите, что три входа и три целевых вектора заданы как

P = [4 5 6];
T = [1.5 3.6 6.7];

Можно теперь получить GRNN с

net = newgrnn(P,T);

и симулируйте его с

P = 4.5;
v = sim(net,P);

Вы можете хотеть попробовать demogrn1. Это показывает, как аппроксимировать функцию GRNN.