zpkshiftc

Комплекс нулей, полюсов и усиления переключает преобразование частоты

Синтаксис

[Z2,P2,K2,AllpassNum,AllpassDen] = zpkshiftc(Z,P,K,Wo,Wt) [Num,Den,AllpassNum,AllpassDen] = zpkshiftc(Z,P,K,0,0.5) [Num,Den,AllpassNum,AllpassDen] = zpkshiftc(Z,P,K,0,-0.5)

Описание

[Z2,P2,K2,AllpassNum,AllpassDen] = zpkshiftc(Z,P,K,Wo,Wt) возвращает нули, Z₂, полюса, P₂, и фактор усиления, K₂, целевого фильтра, преобразованного от действительного lowpass, моделируют путем применения комплексного преобразования сдвига частоты первого порядка. Это преобразование вращает все функции исходного фильтра по той же сумме, заданной местоположением выбранной функции прототипного фильтра, первоначально в _Во, размещенном в _весв целевом фильтре.

Это также возвращает числитель, AllpassNum, и знаменатель, AllpassDen, из allpass, сопоставляющего фильтр. Прототип фильтр lowpass дан с нулями, Z, полюса, P, и фактор усиления, K.

[Num,Den,AllpassNum,AllpassDen] = zpkshiftc(Z,P,K,0,0.5) выполняет Гильбертово преобразование, т.е. 90 степеней против часовой стрелки вращение исходного фильтра в частотном диапазоне.

[Num,Den,AllpassNum,AllpassDen] = zpkshiftc(Z,P,K,0,-0.5) выполняет обратное Гильбертово преобразование, т.е. 90 степеней по часовой стрелке вращение исходного фильтра в частотном диапазоне.

Примеры

Спроектируйте прототип действительный БИХ-полуленточный фильтр с помощью стандартного эллиптического подхода:

[b, a] = ellip(3,0.1,30,0.409);
z = roots(b);
p = roots(a);
k = b(1);

Вращение π/4 Радианами/Выборкой

Вращение-0.25:

[z2,p2,k2] = zpkshiftc(z, p, k, 0.5, 0.25);
hfvt = fvtool(b,a,k2*poly(z2),poly(p2));

Вращение π/2 Радианами/Выборкой

[z3,p3,k3] = zpkshiftc(z, p, k, 0, 0.5);
addfilter(hfvt,k3*poly(z3),poly(p3));
legend(hfvt,'Original Filter','Rotation by -\pi/4 radians/sample',...
    'Rotation by \pi/2 radians/sample');

Вращение Радианами/Выборкой –π/2

[z2,p2,k2] = zpkshiftc(z, p, k, 0.5, -0.5);
fvtool(b, a, k2*poly(z2), poly(p2));

Результат примера 1

После выполнения вращения получившийся фильтр показывает желаемые функции.

Результат примера 2

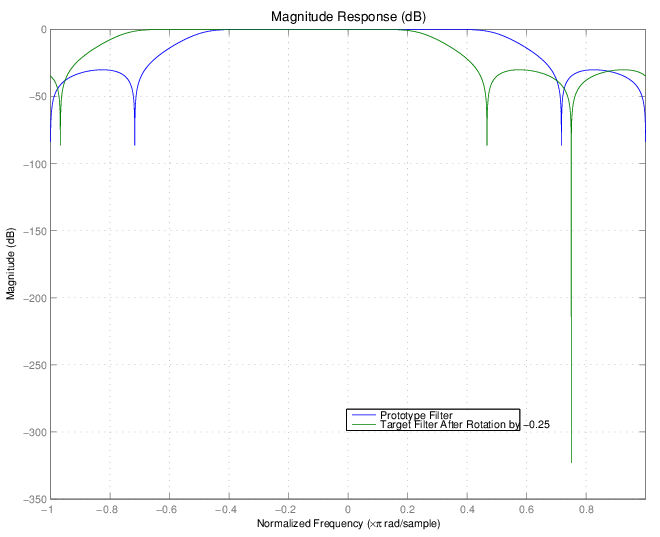
Подобно первому примеру, выполняя Гильбертово преобразование генерирует желаемый целевой фильтр, показанный здесь.

Результат примера 3

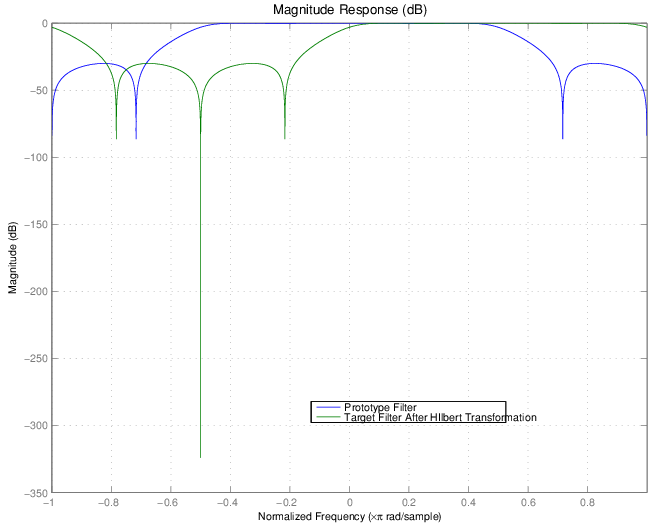
Наконец, использование обратного Гильбертова преобразования создает все же третий фильтр, когда рисунок показывает.

Аргументы

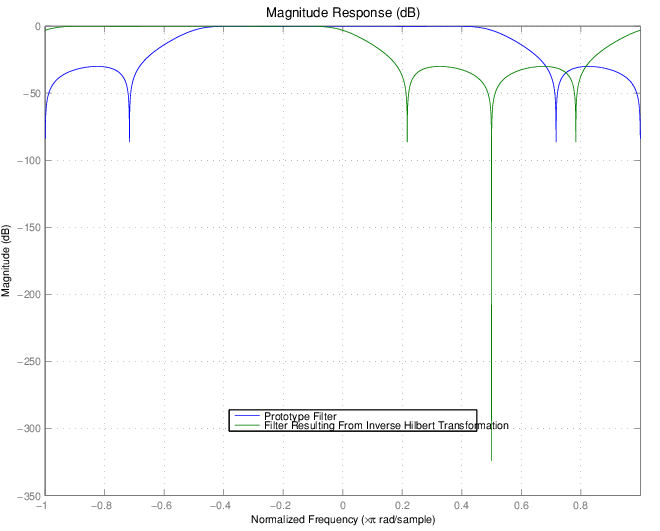
Переменная	Описание
`Z`	Нули прототипа фильтр lowpass
`P`	Полюса прототипа фильтр lowpass
`K`	Фактор усиления прототипа фильтр lowpass
`Wo`	Значение частоты, которое будет преобразовано от прототипного фильтра
`Wt`	Желаемое местоположение частоты в преобразованном целевом фильтре
`Z2`	Нули целевого фильтра
`P2`	Полюса целевого фильтра
`K2`	Фактор усиления целевого фильтра
`AllpassDen`	Числитель фильтра отображения
`AllpassDen`	Знаменатель фильтра отображения

Частоты должны быть нормированы, чтобы быть между-1 и 1 с 1 соответствием половине частоты дискретизации.

Ссылки

Оппенхейм, A.V., Р.В. Шафер и Дж.Р. Бак, обработка сигналов дискретного времени, Prentice-Hall International Inc., 1989.

Датта-Рой, Южная Каролина и Б. Кумар, “На цифровых дифференциаторах, Гильбертовых преобразователях и полуполосе фильтры lowpass”, IEEE^® Transactions на Образовании, издании 32, стр 314-318, август 1989.

Документация