Среднее значение и ковариация неполных многомерных нормальных данных
[Mean,Covariance] = ecmnmle(Data,InitMethod,MaxIterations,Tolerance,Mean0,Covar0)
[Mean,Covariance] = ecmnmle(Data,InitMethod,MaxIterations,Tolerance,Mean0,Covar0) оценивает среднее значение и ковариацию набора данных. Если набор данных имеет отсутствующие значения, эта стандартная программа реализует алгоритм ECM Мэна и Рубина [2] с улучшениями Секстоном и Свенсеном [3]. ECM обозначает условную максимизацию ожидания, условную форму максимизации алгоритма EM Демпстера, Лэрда и Рубина [4].
Эта стандартная программа имеет два операционных режима.
Без выходных аргументов этот режим отображает сходимость алгоритма ECM. Это оценивает и строит значения целевой функции для каждой итерации алгоритма ECM до завершения, как показано в следующем графике.
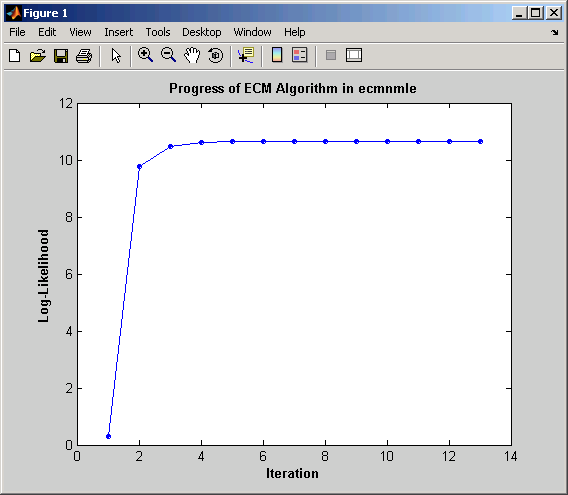
Режим отображения может определить MaxIter и Tolerance значения или служат диагностическим инструментом. Целевая функция является отрицательной функцией логарифмической правдоподобности наблюдаемых данных, и сходимость к оценке наибольшего правдоподобия соответствует минимизации цели.
С выходными аргументами этот режим оценивает среднее значение и ковариацию с помощью алгоритма ECM.
Видеть пример того, как использовать ecmnmle, запустите программу ecmguidemo.
[1] Мало, Родерик Дж. А. и Дональд Б. Рубин. Статистический анализ с Недостающими данными. 2-й выпуск. John Wiley & Sons, Inc., 2002.
[2] Мэн, Xiao-литий и Дональд Б. Рубин. “Оценка Наибольшего правдоподобия с помощью Алгоритма ECM”. Biometrika. Издание 80, № 2, 1993, стр 267–278.
[3] Дьячок, Джо и Андерс Риг Свенсен. “Алгоритмы ECM, которые Сходятся по курсу EM”. Biometrika. Издание 87, № 3, 2000, стр 651–662.
[4] Демпстер, A. P. Н. М. Лэрд и Дональд Б. Рубин. “Наибольшее правдоподобие от Неполных данных с помощью Алгоритма EM”. Журнал Королевского Статистического Общества. Серии B, Издание 39, № 1, 1977, стр 1–37.