Решение использовать оборудование фиксированной точки является просто выбором представлять числа в конкретной форме. Это представление часто предлагает преимущества в терминах потребления энергии, размера, использования памяти, скорости и стоимости конечного продукта.
Измерение физического количества может принять много числовых форм. Например, температура кипения воды составляет 100 градусов Цельсия, 212 градусов по Фаренгейту, 373 кельвина, или 671,4 градуса Rankine. Неважно, какой номер дан, физическое количество является точно тем же самым. Числа отличаются, потому что используются четыре различных шкалы.
Известные стандартные шкалы как Цельсия очень удобны для обмена информацией. Однако существуют ситуации, где это целесообразно создавать и использовать уникальные нестандартные шкалы. Эти ситуации обычно включают максимально использующий ограниченный ресурс.
Например, нестандартные шкалы позволяют производителям карты получать максимальную деталь о листке бумаги фиксированного размера. Типичный дорожный атлас США покажет каждое состояние на 2D отображении страницы. Шкала дюймов к милям будет уникальна для большинства состояний. При помощи большого отношения миль к дюймам весь Техас может соответствовать на двух страницах. Используя ту же шкалу для Род-Айленда сделал бы плохое использование страницы. Используя намного меньшее отношение миль к дюймам позволил бы Род-Айленду быть показанным с максимальной возможной деталью.
Подходящие измерения переменной во встраиваемом процессоре похожи на подбор кривой карте состояния на листке бумаги. Шкала карты должна позволить всем контурам состояния соответствовать на странице. Точно так же двоичная система счисления для измерения должна позволить максимальным и минимальным возможным значениям соответствовать. Шкала карты должна также максимально использовать бумагу для того, чтобы получить максимальную деталь. Точно так же двоичная система счисления для измерения должна максимально использовать процессор для того, чтобы получить максимальную точность.
Использование стандартных шкал для измерений имеет определенные преимущества совместимости. Однако существуют времена, когда стоит повредить соглашение и использовать уникальную нестандартную шкалу. Существуют также случаи, когда соединение уникальности и совместимости целесообразно. Смотрите разделы, которые следуют для получения дополнительной информации.
Предположим, что вы хотите сделать измерения температуры жидкой воды, и что вы хотите представлять эти измерения с помощью 8-битного беззнакового целого. К счастью, диапазон температур жидкой воды ограничивается. Неважно, что масштабирует вас использование, жидкая вода может только пойти от температуры замерзания до точки кипения. Поэтому это - область значений температур, что необходимо получить использование только 256 возможных 8-битных значений: 0,1,2..., 255.
Один подход к представлению температур должен использовать стандартную шкалу. Например, модули для целых чисел могли быть Цельсия. Следовательно, целые числа 0 и 100 представляют воду в температуре замерзания и в точке кипения, соответственно. На позитивном аспекте эта шкала дает тривиальное преобразование от целых чисел до градусов Цельсия. На оборотной стороне числа 101 - 255 не использованы. При помощи этой стандартной шкалы были потрачены впустую больше чем 60% области значений номера.
Второй подход должен использовать нестандартную шкалу. В этой шкале целые числа 0 и 255 представляют воду в температуре замерзания и в точке кипения, соответственно. На позитивном аспекте эта шкала дает максимальную точность, поскольку существует 254 значения между замораживанием и кипением вместо всего 99. На оборотной стороне модули являются примерно 0,3921568 степенями Цельсия на бит, таким образом, преобразование в Цельсия требует деления 2,55, который является относительно дорогой операцией на большинстве процессоров фиксированной точки.
Третий подход должен использовать “полустандартную” шкалу. Например, целые числа 0 и 200 могли представлять воду в температуре замерзания и в точке кипения, соответственно. Модули для этой шкалы составляют 0,5 градуса Цельсия за бит. На оборотной стороне эта шкала не использует числа от 201 до 255, который представляет трату больше чем 21%. На позитивном аспекте эта шкала разрешает относительно легкое преобразование в стандартную шкалу. Преобразование в Цельсия вовлекает деление 2, который является очень легкой операцией сдвига на большинстве процессоров.
Одна из ключевых операций в преобразовании от одной шкалы до другого является умножением. Предыдущее тематическое исследование дало три примера преобразований из квантованного целочисленного значения Q к реальному значению Цельсия V, который включил только умножение:
Графически, преобразование является линией с наклонным S, который должен пройти через источник. Линия через начало координат называется чисто линейным преобразованием. Ограничение себя к чисто линейному преобразованию может быть очень расточительным, и часто лучше использовать общее уравнение линии:
V = SQ + B.
Путем добавления смещения называют B, можно получить большую точность при квантовании к ограниченному количеству битов.
Общее уравнение линии дает очень полезное преобразование в квантованную шкалу. Однако как все методы квантования, точность ограничивается, и ошибки могут быть введены преобразованием. Общим уравнением линии с ошибкой квантования дают
Если квантованное значение Q округлено к самому близкому представимому номеру, то
Таким образом, количество ошибки квантования определяется и количеством битов и шкалой. Этот сценарий представляет ошибку лучшего случая. Для других схем округления ошибка может быть вдвое более большой.
На типичных электронно управляемых двигателях внутреннего сгорания поток топлива отрегулирован, чтобы получить желаемое отношение воздуха к топливу в цилиндрах только до сгорания. Поэтому знание текущего уровня воздушного потока требуется. Некоторые производители используют датчики, которые непосредственно измеряют воздушный поток, в то время как другие производители вычисляют воздушный поток от измерений связанных сигналов. Отношение этих переменных выведено из идеального газового уравнения. Идеальное газовое уравнение вовлекает деление температурой воздуха. Для соответствующих результатов шкала абсолютной температуры, таких как кельвин или Rankine должна использоваться в уравнении. Однако квантование непосредственно к шкале абсолютной температуры вызвало бы напрасно большие ошибки квантования.
Температура воздуха, текущего в механизм, имеет ограниченный диапазон. На типичном механизме теплоотвод спроектирован, чтобы сохранить блок ниже температуры кипения охлаждающейся жидкости. Примите максимум 225oF (380 K). Как воздушные потоки через впускной коллектор, это может быть нагрето к этой максимальной температуре. Для холодного запуска в экстремальном климате температура может быть всего-60oF (222 K). Поэтому с помощью абсолютной шкалы кельвина, область значений интереса является 222 K к 380 K.
Температура воздуха должна быть квантована для обработки встроенной системой управления. Принятие нереалистичного квантования к 3-битным числам без знака: 0,1,2..., 7, чисто линейное преобразование с максимальной точностью
Квантованное преобразование и область значений интереса показывают в следующем рисунке.
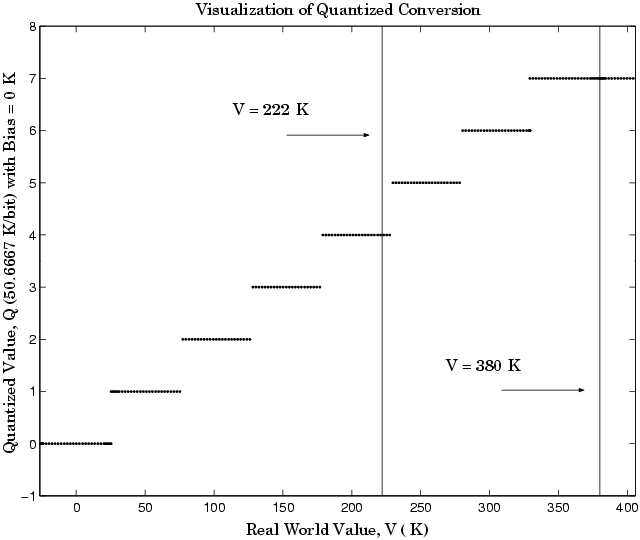
Заметьте, что существует 7,5 возможных значений квантования. Это вызвано тем, что только половина первого бита соответствует температурам (реальные значения) больше, чем нуль.
Ошибка квантования является –25.33 K/bit ≤ Error ≤ 25.33 K/bit.
Область значений интереса квантованного преобразования и абсолютного значения квантованной ошибки показывают в следующем рисунке.
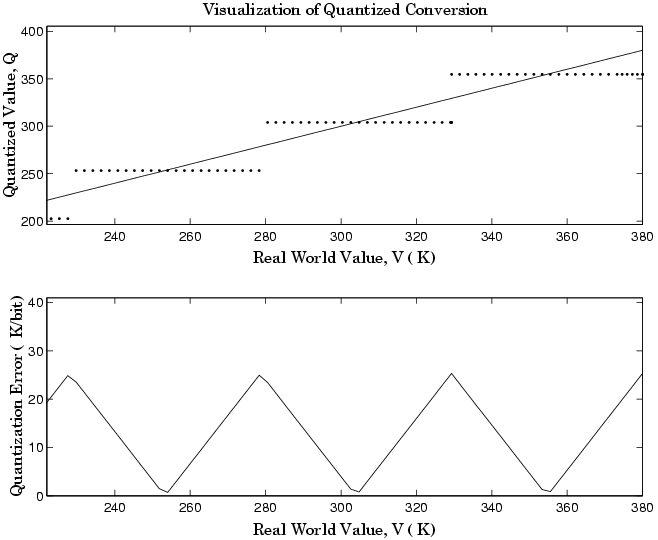
Как альтернатива чисто линейному преобразованию, рассмотрите общее линейное преобразование с максимальной точностью:
Квантованное преобразование и область значений интереса показывают в следующем рисунке.
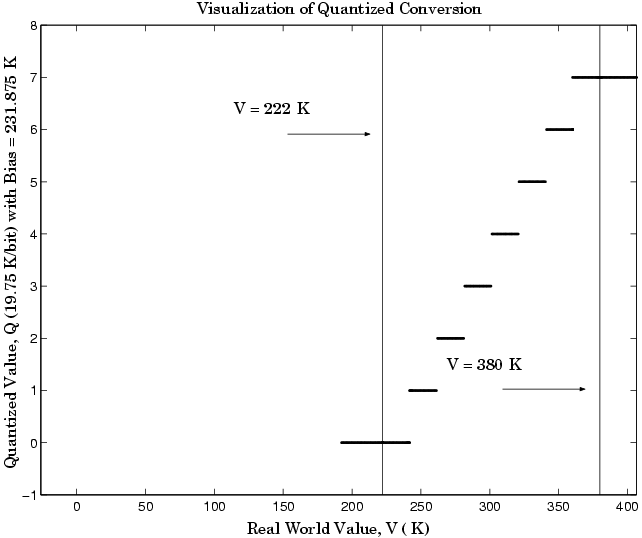
Ошибка квантования является-9.875 K/bit ≤ Error ≤ 9.875 K/bit, который приблизительно в 2.5 раза меньше, чем ошибка, сопоставленная с чисто линейным преобразованием.
Область значений интереса квантованного преобразования и абсолютного значения квантованной ошибки показывают в следующем рисунке.
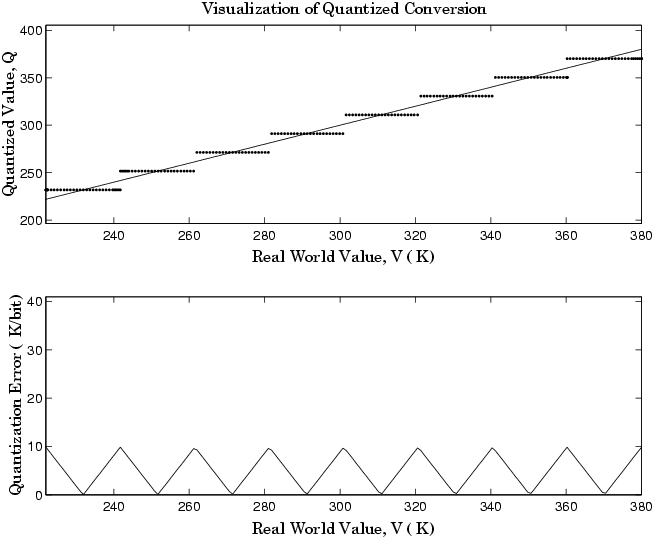
Безусловно, общая линейная шкала дает намного лучшую точность, чем чисто линейная шкала в области значений интереса.