Квантование

Квантование Q реального значения V представлено взвешенной суммой битов. В контексте общего наклона и схемы кодирования смещения, значением количества фиксированной точки без знака дают

$\tilde{V} = S . [\sum_{i = 0}^{w s - 1} b_{i} 2^{i}] + B,$

в то время как значением количества фиксированной точки со знаком дают

$\tilde{V} = S . [- b_{w s - 1} 2^{w s - 1} + \sum_{i = 0}^{w s - 2} b_{i} 2^{i}] + B,$

где

$b_{i}$ двоичные цифры, с $b_{i} = 1, 0$ для $i = 0, 1, ..., w s - 1$
Размер слова в битах дан ws с ws = 1, 2, 3,..., 128.
S дают $F = 2^{E}$ , где масштабирование неограниченно, потому что двоичная точка не должна быть непрерывной со словом.

$b_{i}$ называются битными множителями и $2^{i}$ называются весами.

Формат фиксированной точки

Форматы для 8-битных значений фиксированной точки без знака и со знаком показывают в следующем рисунке.

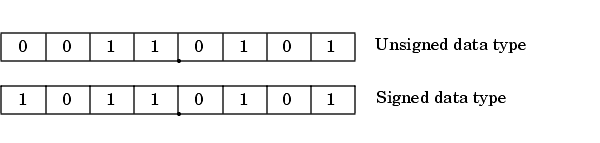
Обратите внимание на то, что вы не можете различить, подписываются ли эти числа или типы данных без знака просто контролем, поскольку эта информация явным образом не закодирована в слове.

Двоичное число 0011.0101 дает к тому же значению для дополнительного представления и two без знака потому что MSB = 0. Установка B = 0 и с помощью соответствующих весов, битных множителей и масштабирования, значение

$\begin{matrix} \tilde{V} = (F 2^{E}) Q = 2^{E} [\sum_{i = 0}^{w s - 1} b_{i} 2^{i}] \\ = 2^{- 4} (0 \times^{27} + 0 \times^{26} + 1 \times^{25} + 1 \times^{24} + 0 \times^{23} + 1 \times^{22} + 0 \times^{21} + 1 \times^{20}) \\ = 3.3125. \end{matrix}$

С другой стороны, двоичное число 1011.0101 дает к различным значениям для дополнительного представления и two без знака начиная с MSB = 1.

Установка B = 0 и с помощью соответствующих весов, битных множителей и масштабирования, значение без знака

$\begin{matrix} \tilde{V} = (F 2^{E}) Q = 2^{E} [\sum_{i = 0}^{w s - 1} b_{i} 2^{i}] \\ = 2^{- 4} (1 \times^{27} + 0 \times^{26} + 1 \times^{25} + 1 \times^{24} + 0 \times^{23} + 1 \times^{22} + 0 \times^{21} + 1 \times^{20}) \\ = 11.3125, \end{matrix}$

в то время как дополнительное значение two

$\begin{matrix} \tilde{V} = (F 2^{E}) Q = 2^{E} [- b_{w s - 1} 2^{w s - 1} + \sum_{i = 0}^{w s - 2} b_{i} 2^{i}] \\ = 2^{- 4} (- 1 \times^{27} + 0 \times^{26} + 1 \times^{25} + 1 \times^{24} + 0 \times^{23} + 1 \times^{22} + 0 \times^{21} + 1 \times^{20}) \\ = - 4.6875. \end{matrix}$

Документация Fixed-Point Designer

Поддержка

Памятка переводчика

1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.

2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.

3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.

4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.

5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.