Линейная и Нелинейная Ограниченная Минимизация Используя patternsearch

Линейная и нелинейная ограниченная минимизация Используя `patternsearch`

Линейно ограниченная проблема

Описание проблемы

Этот раздел представляет пример выполнения поиска шаблона на ограниченной проблеме минимизации. Пример минимизирует функцию

$F (x) = \frac{}{12} x^{T} H x + f^{T} x,$

где

$\begin{matrix} H = [\begin{matrix} 36 & 17 & 19 & 12 & 8 & 15 \\ 17 & 33 & 18 & 11 & 7 & 14 \\ 19 & 18 & 43 & 13 & 8 & 16 \\ 12 & 11 & 13 & 18 & 6 & 11 \\ 878698 \\ 15 & 14 & 16 & 11 & 8 & 29 \end{matrix}], \\ f = [\begin{matrix} 20 & 15 & 21 & 18 & 29 & 24 \end{matrix}], \end{matrix}$

удовлетворяющее ограничениям

$\begin{matrix} A \cdot x \leq b, \\ A e q \cdot x = b e q, \end{matrix}$

где

$\begin{matrix} A = [\begin{matrix} - 8 & 73 & - 4 & 90 \end{matrix}], \\ b = 7, \\ A e q = [\begin{matrix} 71833350 & - 5 & 1 & - 5 & 8 \\ - 2 & - 6 \\ 71191 & - 1 & 2 & - 2 & 3 & - 3 \end{matrix}], \\ b e q = [\begin{matrix} 84 & 62 & 65 & 1 \end{matrix}] . \end{matrix}$

Выполнение поиска шаблона на примере

Чтобы выполнить поиск шаблона на примере, сначала войдите

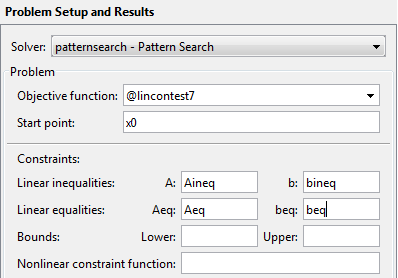
optimtool('patternsearch')

открыть приложение Оптимизации или ввести optimtool и затем выберите patternsearch в меню Solver. Затем введите следующую функцию в поле Objective function:

@lincontest7

lincontest7 файл, включенный в программное обеспечение Global Optimization Toolbox, которое вычисляет целевую функцию для примера. Поскольку матрицы и векторы, задающие начальную точку и ограничения, являются большими, более удобно установить их значения как переменные в рабочей области MATLAB^® сначала и затем ввести имена переменных в приложение Оптимизации. Для этого войдите

x0 = [2 1 0 9 1 0];
Aineq = [-8 7 3 -4 9 0];
bineq = 7;
Aeq = [7 1 8 3 3 3; 5 0 -5 1 -5 8; -2 -6 7 1 1 9; 1 -1 2 -2 3 -3];
beq = [84 62 65 1];

Затем введите следующее в приложение Оптимизации:

Установите Start point на x0.
Установите следующий Linear inequalities:
- Установите A на Aineq.
- Установите b на bineq.
- Установите Aeq на Aeq.
- Установите beq на beq.

Следующий рисунок показывает эти настройки в приложении Оптимизации.

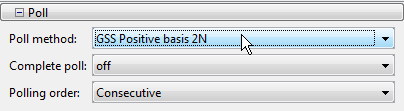
Поскольку это - линейно ограниченная проблема, установите Poll method на GSS Positive basis 2N. Для получения дополнительной информации о КПД методов поиска GSS для линейно ограниченных проблем, смотрите, Сравнивают КПД Опций Опроса.

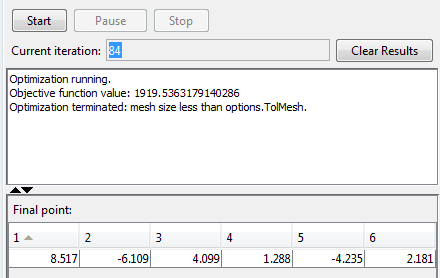
Затем нажмите Start, чтобы запустить поиск шаблона. Когда поиск закончен, результаты отображены в панели Run solver and view results как показано в следующем рисунке.

Запускать эту проблему с помощью функций командной строки:

x0 = [2 1 0 9 1 0];
Aineq = [-8 7 3 -4 9 0];
bineq = 7;
Aeq = [7 1 8 3 3 3; 5 0 -5 1 -5 8; -2 -6 7 1 1 9; 1 -1 2 -2 3 -3];
beq = [84 62 65 1];
options = optimoptions('patternsearch',...
    'PollMethod','GSSPositiveBasis2N');
[x,fval,exitflag,output] = patternsearch(@lincontest7,x0,... 
   Aineq,bineq,Aeq,beq,[],[],[],options);

Просмотрите решение, значение целевой функции и количество функциональных оценок во время процесса решения.

x,fval,output.funccount

x =

    8.5165   -6.1094    4.0989    1.2877   -4.2348    2.1812


fval =

   1.9195e+03


ans =

   758

Нелинейно ограниченная проблема

Предположим, что вы хотите минимизировать простую целевую функцию двух переменных x1 и x2,

$\min_{x} f (x) = (4 - 2.1 x_{1}^{2} - x_{1}^{4 / 3}) x_{1}^{2} + x_{1} x_{2} + (- 4 + 4 x_{2}^{2}) x_{2}^{2}$

подвергните следующим нелинейным ограничениям неравенства и границам

$\begin{array}{l} x_{1} x_{2} + x_{1} - x_{2} + 1.5 \leq 0 & (нелинейное ограничение) \\ 10 - x_{1} x_{2} \leq 0 & (нелинейное ограничение) \\ 0 \leq x_{1} \leq 1 & (связанный) \\ 0 \leq x_{2} \leq 13 & (связанный) \end{array}$

Начните путем создания ограничительных функций и цели. Во-первых, создайте файл с именем simple_objective.m можно следующим образом:

function y = simple_objective(x)
y = (4 - 2.1*x(1)^2 + x(1)^4/3)*x(1)^2 + x(1)*x(2) + (-4 + 4*x(2)^2)*x(2)^2;

Решатель поиска шаблона принимает, что целевая функция возьмет один вход x где x имеет столько же элементов сколько количество переменных в проблеме. Целевая функция вычисляет значение функции и возвращает то скалярное значение в его одном возвращаемом аргументе y.

Затем создайте файл с именем simple_constraint.m содержа ограничения:

function [c, ceq] = simple_constraint(x)
c = [1.5 + x(1)*x(2) + x(1) - x(2);
-x(1)*x(2) + 10];
ceq = [];

Решатель поиска шаблона принимает, что ограничительная функция возьмет один вход x, где x имеет столько же элементов сколько количество переменных в проблеме. Ограничительная функция вычисляет значения всех ограничений неравенства и ограничений равенства и возвращает два вектора, c и ceq, соответственно.

Затем минимизировать целевую функцию с помощью patternsearch функция, необходимо передать в указателе на функцию целевой функции, а также определению стартовой точки в качестве второго аргумента. Нижние и верхние границы обеспечиваются как LB и UB соответственно. Кроме того, также необходимо передать указатель на функцию нелинейной ограничительной функции.

ObjectiveFunction = @simple_objective;
X0 = [0 0];   % Starting point
LB = [0 0];   % Lower bound
UB = [1 13];  % Upper bound
ConstraintFunction = @simple_constraint;
[x,fval] = patternsearch(ObjectiveFunction,X0,[],[],[],[],...
                         LB,UB,ConstraintFunction)

Optimization terminated: mesh size less than options.MeshTolerance
 and constraint violation is less than options.ConstraintTolerance.

x =
    0.8122   12.3122

fval =
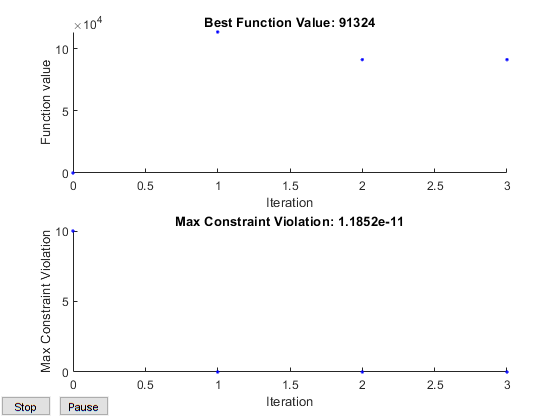
  9.1324e+004

Затем постройте результаты. Создайте опции с помощью optimoptions это выбирает две функции построения графика. Первая функция построения графика psplotbestf строит лучшее значение целевой функции в каждой итерации. Вторая функция построения графика psplotmaxconstr строит максимальное ограничительное нарушение в каждой итерации.

Примечание

Можно также визуализировать прогресс алгоритма путем отображения информации к Командному окну с помощью 'Display' опция.

options = optimoptions('patternsearch','PlotFcn',{@psplotbestf,@psplotmaxconstr},'Display','iter');
[x,fval] = patternsearch(ObjectiveFunction,X0,[],[],[],[],LB,UB,ConstraintFunction,options)

                                      Max
  Iter   Func-count       f(x)      Constraint   MeshSize      Method
    0         1            0           10       0.8919    
    1        28       113580            0        0.001   Increase penalty
    2       105        91324    1.782e-07        1e-05   Increase penalty
    3       192        91324    1.188e-11        1e-07   Increase penalty
Optimization terminated: mesh size less than options.MeshTolerance
 and constraint violation is less than options.ConstraintTolerance.

x =

    0.8122   12.3122


fval =

   9.1324e+04

Лучшее значение целевой функции и максимальное ограничительное нарушение в каждой итерации

Документация