Точный расчет является довольно точным методом для предсказания положения, если транспортное средство может обеспечить запланированный курс. Самолет и поставки могут быть продвинуты от запланированного курса ветрами и током. Важный шаг в навигационном планировании должен вычислить необходимую коррекцию дрейфа.
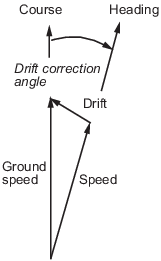
В стандартной проблеме коррекции дрейфа известны желаемый курс и ветер, но заголовок должен был остаться на курсе, неизвестно. Эта проблема хорошо подходит для векторного анализа. Скорость ветра является вектором известной величины и направления. Скорость транспортного средства относительно движущейся массы воздуха является вектором известной величины, но неизвестным направлением. Этот заголовок должен быть выбран так, чтобы сумма транспортного средства и скоростей ветра дала результант в заданном направлении курса. Скорость относительно земли может быть больше или меньшей, чем воздушная скорость из-за компонентов попутного ветра или встречного ветра. Навигатор хотел бы знать необходимый заголовок, связанный угол коррекции ветра и получившуюся скорость относительно земли.
Какой заголовок помещает самолет на курс 250 °, когда ветер составляет 38 узлов от 285 °? Самолет летит в скорости полета 145 узлов.
course = 250; airspeed = 145; windfrom = 285; windspeed = 38;
[heading,groundspeed,windcorrangle] = ...
driftcorr(course,airspeed,windfrom,windspeed)
heading =
258.65
groundspeed =
112.22
windcorrangle =
8.65Необходимый заголовок составляет приблизительно 9 ° справа от курса. Существует компонент встречного ветра на 33 узла.
Связанной проблемой является расчет скорости ветра и направления из наблюдаемого заголовка и курса. Скорость ветра является только векторной разностью скорости относительно земли и скорости относительно массы воздуха.
[windfrom,windspeed] = ...
driftvel(course,groundspeed,heading,airspeed)windfrom =
285.00
windspeed =
38.00