Площадь поверхности многоугольника на сфере или эллипсоиде
area = areaint(lat,lon)
area = areaint(lat,lon,ellipsoid)
area = areaint(lat,lon,units)
area = areaint(lat,lon,ellipsoid,units)
area = areaint(lat,lon) вычисляет сферическую площадь поверхности многоугольника, заданного входными векторами lat и lon. Вычисление использует подход линейного интеграла. Выход, area, часть площади поверхности, покрытой многоугольником на сфере единичного радиуса. Чтобы предоставить несколько многоугольников, разделите многоугольники NaNs во входных векторах. Точность метода интегрирования обратно пропорциональна расстоянию между точками lat/lon.
area = areaint(lat,lon,ellipsoid) вычисляет площадь поверхности многоугольника на эллипсоиде или сфере, заданной входом ellipsoid, который может быть referenceSphere, referenceEllipsoid, или oblateSpheroid объект или вектор формы [semimajor_axis eccentricity]. Выход, area, находится в модулях квадратов, соответствующих модулям ellipsoid.
area = areaint(lat,lon,units) использует модули, заданные units, скаляр строки или вектор символов 'degrees' или 'radians'. Если не использовано, модули по умолчанию степеней приняты.
area = areaint(lat,lon,ellipsoid,units) использование оба входные параметры ellipsoid и units в вычислении.
Считайте область заключенной 30º двуугольник от полюса до полюса и ограниченный главным меридианом и 30ºE. Можно использовать функциональный areaquad получить точное решение:
area = areaquad(90,0,-90,30)
area =
0.0833Это - 1/12 сферическая область. Чем больше точек раньше задавало этот многоугольник, тем больше этапов интеграции areaint берет, улучшая оценку. Эта первая попытка берет точку каждый 30º широты:
lats = [-90:30:90,60:-30:-60]';
lons = [zeros(1,7), 30*ones(1,5)]';
area = areaint(lats,lons)
area =
0.0792Теперь вычислите лучшую оценку с одной точкой каждый 1º широты:
lats = [-90:1:90,89:-1:-89]';
lons = [zeros(1,181), 30*ones(1,179)]';
area = areaint(lats,lons)
area =
0.0833Эта функция включает измерение областей, заключенных произвольными многоугольниками. Это - числовая оценка, с помощью линейного интеграла на основе Теоремы Зеленого. По сути, это ограничивается точностью и разрешением входных данных.
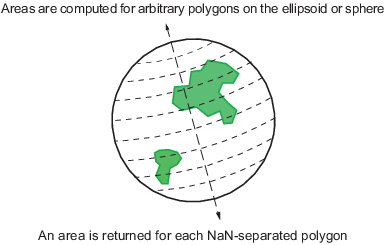
Учитывая достаточные данные, areaint функция является лучшим методом для определения областей комплексных многоугольников, таких как континенты, облачный покров и другие естественные или выведенные функции. Вычисления в этой функциональной работе сферическое Наземное предположение. Для несферических эллипсоидов данные о широте преобразованы во вспомогательную authalic сферу.