intersectgeoquad

Пересечение двух четырехугольников долготы широты

Синтаксис

[latlim, lonlim] = intersectgeoquad(latlim1, lonlim1, latlim2, lonlim2)

Описание

[latlim, lonlim] = intersectgeoquad(latlim1, lonlim1, latlim2, lonlim2) вычисляет пересечение четырехугольника, заданного широтой, и долгота ограничивает latlim1 и lonlim1, с четырехугольником, заданным широтой и долготой, ограничивает latlim2 и lonlim2. latlim1 и latlim2 двухэлементные векторы формы [southern-limit northern-limit]. Аналогично, lonlim1 и lonlim2 двухэлементные векторы формы [western-limit eastern-limit]. Все углы ввода и вывода находятся в модулях степеней. Перекрестные результаты даны в выходных массивах latlim и lonlim. Учитывая произвольную пару входных четырехугольников, существует три возможных результата:

Четырехугольникам не удается пересечься. В этом случае, оба latlim и lonlim пустые массивы.
Пересечение состоит из одного четырехугольника. В этом случае, latlim (как latlim1 и latlim2) двухэлементный вектор, который имеет форму [southern-limit northern-limit], где southern-limit и northern-limit представляйте скалярные значения. lonlim (как lonlim1 и lonlim2), двухэлементный вектор, который имеет форму [western-limit eastern-limit], с парой скалярных пределов.
Пересечение состоит из пары четырехугольников. Это может произойти, когда долготы повторяются таким образом, что восточный конец одного четырехугольника перекрывает западный конец другой и наоборот. Например, если lonlim1 = [-90 90] и lonlim2 = [45 -45], существует два интервала перекрытия: [-90 -45] и [45 90]. Эти пределы возвращены в lonlim в отдельных строках, формируя массив 2 на 2. В нашем примере (принимающий, что широта ограничивает перекрытие), lonlim равнялся бы [-90 -45; 45 90]. Это все еще имеет форму [western-limit eastern-limit], но western-limit и eastern-limit 2 1, а не скаляр. Два выходных четырехугольника имеют те же пределы широты, но они реплицированы так, чтобы latlim также 2 на 2.
Продолжать пример, если latlim1 = [0 30] и latlim2 = [20 50]latlim равняется [20 30; 20 30]. Формой является все еще [southern-limit northern-limit], но в этом случае southern-limit и northern-limit 2 1.

Примеры

Пример 1

Непересечение четырехугольников:

[latlim, lonlim] = intersectgeoquad( ...
                   [-40 -60], [-180 180], [40 60], [-180 180])
latlim =
     []

lonlim =
     []

Пример 2

Пересечение является одним четырехугольником:

[latlim, lonlim] = intersectgeoquad( ...
                   [-40 60], [-120 45], [-60 40], [160 -75])

latlim =
   -40    40

lonlim =
  -120   -75

Пример 3

Пересечение является парой четырехугольников:

[latlim, lonlim] = intersectgeoquad( ...
                   [-30 90],[-10 -170],[-90 30],[170 10])
 
latlim =
   -30    30
   -30    30

lonlim =
   -10    10
   170  -170

Пример 4

Входные параметры и выход полностью окружают планету:

[latlim, lonlim] = intersectgeoquad( ...
                   [-30 90],[-180 180],[-90 30],[0 360])

latlim =
   -30    30

lonlim =
  -180   180

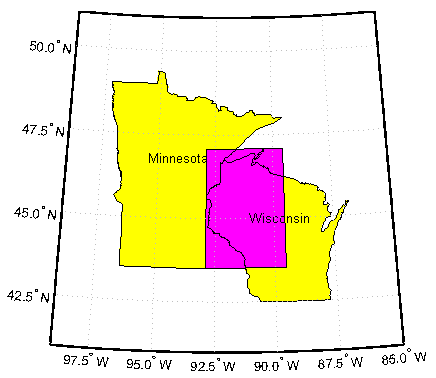
Пример 5

Найдите и сопоставьте пересечение ограничительных рамок смежных штатов США:

usamap({'Minnesota','Wisconsin'})
S = shaperead('usastatehi','UseGeoCoords',true,'Selector',...
    {@(name) any(strcmp(name,{'Minnesota','Wisconsin'})), 'Name'});
geoshow(S, 'FaceColor', 'y')
textm([S.LabelLat], [S.LabelLon], {S.Name},...
    'HorizontalAlignment', 'center')
latlimMN = S(1).BoundingBox(:,2)'

latlimMN =
   43.4995   49.3844

lonlimMN = S(1).BoundingBox(:,1)'

lonlimMN =
  -97.2385  -89.5612

latlimWI = S(2).BoundingBox(:,2)'

latlimWI =
   42.4918   47.0773

lonlimWI = S(2).BoundingBox(:,1)'

lonlimWI =
  -92.8892  -86.8059

[latlim lonlim] = ...
    intersectgeoquad(latlimMN, lonlimMN, latlimWI, lonlimWI)

latlim =
   43.4995   47.0773

lonlim =
  -92.8892  -89.5612

geoshow(latlim([1 2 2 1 1]), lonlim([1 1 2 2 1]), ...
    'DisplayType','polygon','FaceColor','m')

Советы

latlim1 и latlim2 должен обычно даваться в порядке увеличения численного значения. Никакая ошибка не закончится если, например, latlim1(2) < latlim1(1), но выходные параметры оба будут пустыми массивами.

Никакое такое ограничение не применяется к lonlim1 и lonlim2. Первый элемент всегда интерпретируется как западный предел, даже если это превышает второй элемент (восточный предел). Кроме того, intersectgeoquad правильно указатели безотносительно переносящего долготу соглашения, возможно, были применены к lonlim1 и lonlim2.

В терминах выхода, intersectgeoquad переносит lonlim таким образом, что все элементы падают в закрытом интервале [-180 180]. Это означает, что, если (один из) выходной четырехугольник (четырехугольники) пересекает меридиан на 180 °, его западный предел превышает его восточный предел. Результат был бы таков что

lonlim(2) < lonlim(1)

если пересечение включает один четырехугольник или

lonlim(k,2) < lonlim(k,1)

где k равняется 1 или 2, если пересечение включает пару четырехугольников.

Если abs(diff(lonlim1)) или abs(diff(lonlim2)) равняется 360, его четырехугольник интерпретирован как широтная зона, которая полностью окружает планету, ограниченную только одной параллелью на юге и другой параллелью на севере. Если два таких четырехугольника пересекаются, lonlim установлен в [-180 180].

Если вы хотите отобразить географические четырехугольники, сгенерированные этой функцией или кем-либо другим, которые являются больше чем одним или двумя градусами в области степени, они не могут следовать за изогнутыми меридианами и параллелями очень хорошо. Степень отъезда зависит от степени четырехугольника, проекции карты и шкалы карты. В таких случаях можно интерполировать промежуточные вершины вдоль ребер четырехугольника с outlinegeoquad функция.

Смотрите также

ingeoquad | outlinegeoquad

Документация