Интерполируйте между waypoints на обычной сетке данных
[zi,ri,lat,lon] = mapprofile
[zi,ri,lat,lon] = mapprofile(Z,R,lat,lon)
[zi,ri,lat,lon] = mapprofile(Z,R,lat,lon,units)
[zi,ri,lat,lon] = mapprofile(Z,R,lat,lon,ellipsoid)
[zi,ri,lat,lon] = mapprofile(___,'trackmethod','interpmethod')
mapprofile строит профиль значений между waypoints на отображенной обычной сетке данных. mapprofile использует текущий объект, если это - обычная сетка данных или первая обычная сетка данных, найденная на текущей системе координат. zdata сетки используется в профиле. Цветные данные используются в отсутствие zdata. Результат отображен в новой фигуре.
[zi,ri,lat,lon] = mapprofile возвращает значения профиля, не отображая их. Выход zi содержит интерполированные значения вдоль больших кругов между waypoints. ri вектор связанных расстояний сначала waypoint в модулях степеней дуги вдоль поверхности. lat и lon соответствующие широты и долготы.
[zi,ri,lat,lon] = mapprofile(Z,R,lat,lon) принимает как вход обычную сетку данных и waypoint векторы. Никакая отображенная сетка не требуется. Наборы waypoints могут быть разделены NaNs в последовательности линии. Выходные области значений измеряются сначала waypoint в последовательности. R может быть географический объект растровой привязки, вектор ссылки или матрица привязки.
Если R географический объект растровой привязки, его RasterSize свойство должно быть сопоставимо с size(Z).
Если R вектор ссылки, это должно быть 1 3 с элементами:
[cells/degree northern_latitude_limit western_longitude_limit]
Если R матрица привязки, это должно быть 3 2 и преобразовать растровые индексы строки и столбца к или от географических координат согласно:
[lon lat] = [row col 1] * R
Если R матрица привязки, она должна задать (невращательный, нескошенный) отношение, в котором каждый столбец сетки данных падает вдоль меридиана и каждой строки падения вдоль параллели.
[zi,ri,lat,lon] = mapprofile(Z,R,lat,lon,units) задает модули выходных областей значений вдоль профиля. Допустимые модульные входные параметры области значений являются любым значением расстояния, распознанным unitsratio. Поверхностные расстояния вычисляются с помощью радиуса по умолчанию земли. Если не использовано, 'degrees' приняты.
[zi,ri,lat,lon] = mapprofile(Z,R,lat,lon,ellipsoid) использует предоставленное определение эллипсоида в вычислении области значений вдоль профиля. ellipsoid referenceSphere, referenceEllipsoid, или oblateSpheroid объект или вектор формы [semimajor_axis eccentricity]. О выходной области значений сообщают в тех же единицах расстояния как большие полуоси эллипсоида. Если не использовано, вектор области значений для сферы.
[zi,ri,lat,lon] = mapprofile(___,'trackmethod','interpmethod') управляйте используемыми методами интерполяции. Допустимыми методами дорожки является 'gc' поскольку большой круг отслеживает между waypoints и 'rh' для локсодром. Действительными методами для интерполяции в матрице является 'bilinear' для линейной интерполяции, 'bicubic' для кубичной интерполяции и 'nearest' для самой близкой соседней интерполяции. Если не использовано, 'gc' и 'bilinear' приняты.
Создайте карту оси для корейского полуострова. Задайте профиль вертикального изменения через демонстрационные корейские цифровые данные о вертикальном изменении и постройте их, объединенный с маркерами береговой линии и города:
load korea
h = worldmap(map, refvec); % The figure has no map content.
plat = [ 43 43 41 38];
plon = [116 120 126 128];
mapprofile(map, refvec, plat, plon)
load coastlines
plotm(coastlat,coastlon)
geoshow('worldcities.shp', 'Marker', '.', 'Color', 'red')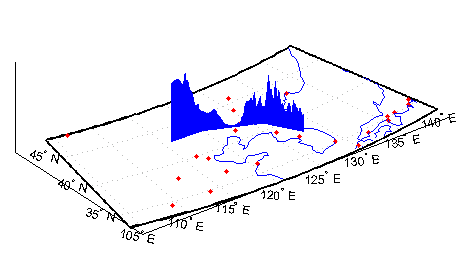
Когда вы выбираете больше чем два waypoints, автоматически сгенерированная фигура отображает результат в трех измерениях. Следующий пример показывает относительные размеры гор в северном Китае по сравнению с глубинами Японского моря. Вызов mapprofile без входных параметров позволяет вам в интерактивном режиме выбрать waypoints на фигуре, использующей мышь. Каждое нажатие кнопки выбирает новый waypoint и хранит значения профиля, но точки не отображены на фигуре. Нажмите Enter после того, как вы выберете конечную точку:
axes(h); meshm(map, refvec, size(map)) demcmap(map) [zi,ri,lat,lon] = mapprofile;
Добавление выходных аргументов подавляет отображение результатов в новой фигуре. Можно затем использовать результаты в дальнейших вычислениях или отобразить результаты сами. Здесь профиль от верхнего левого угла до нижнего правого угла вычисляется из waypoints, в интерактивном режиме выбрал карту (ваш профиль не будет идентичен тому, что показывают ниже). Пример преобразует области значений и вертикальные изменения к километрам и отображает их в новой фигуре, устанавливаясь вертикальный коэффициент преувеличения на 20. Без вертикального преувеличения разницы в вертикальном положении были бы почти слишком малы, чтобы видеть.
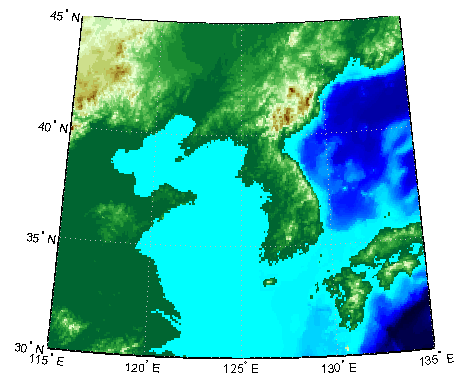
figure plot(deg2km(ri),zi/1000) daspect([ 1 1/20 1 ]); xlabel 'Range (km)' ylabel 'Elevation (km)'
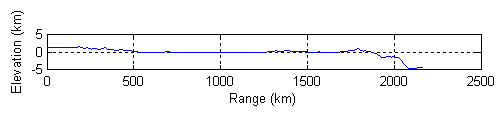
Естественно, профиль, который вы получаете, зависит от местоположений поперечного разреза, которые вы выбираете.
Можно вычислить значения вдоль пути независимо от существующей фигуры путем обеспечения обычной сетки данных и векторов координат waypoint. Дополнительные аргументы позволяют управление модулями области значений выход и методы интерполяции между waypoints и элементами сетки данных.
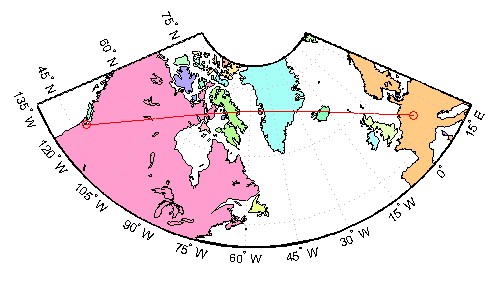
Покажите, какая земля и океанские области лежат под большой круговой дорожкой от Франкфурта до Сиэтла:
cities = shaperead('worldcities.shp', 'UseGeoCoords', true);
Seattle = strcmp('Seattle', {cities(:).Name});
Frankfurt = strcmp('Frankfurt', {cities(:).Name});
lat = [cities(Seattle).Lat cities(Frankfurt).Lat]
lon = [cities(Seattle).Lon cities(Frankfurt).Lon]
load topo
[valp,rp,latp,lonp] = ...
mapprofile(double(topo),topolegend, ...
lat,lon,'km','gc','nearest');
figure
worldmap([40 80],[-135 20])
land = shaperead('landareas.shp', 'UseGeoCoords', true);
faceColors = makesymbolspec('Polygon',...
{'INDEX', [1 numel(land)], 'FaceColor', ...
polcmap(numel(land))});
geoshow(land,'SymbolSpec',faceColors)
plotm(latp,lonp,'r')
plotm(lat,lon,'ro')
axis off