Куб задан восемью вершинами та форма шесть сторон. Этот рисунок показывает x-, y-, и z-координаты вершин, задающих куб, в котором стороны являются одним модулем в длине.
Если вы задаете x-, y-, и аргументы z-координаты как векторы, они представляют как один многоугольник с точками, соединенными в последовательности. Если аргументы являются матрицами, MATLAB® чертит один многоугольник для каждого столбца, производя одну закрашенную фигуру с несколькими поверхностями. Эти поверхности не должны быть соединены и могут самопересекаться.
В качестве альтернативы можно задать координаты каждой уникальной вершины и порядка, в котором можно соединить их, чтобы сформировать поверхности. Примеры в этом разделе иллюстрируют оба метода.
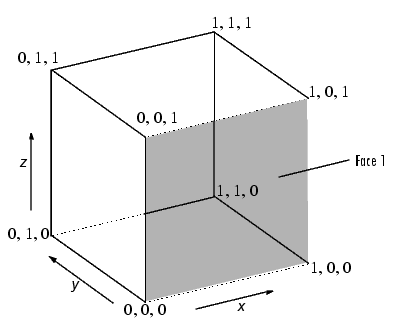
Каждая из шести поверхностей имеет четыре вершины. Поскольку вы не должны закрывать каждый многоугольник (т.е. первые и последние вершины не должны быть тем же самым), можно задать этот куб с помощью 4 6 матрица для каждого из x-, y-, и z-координаты.
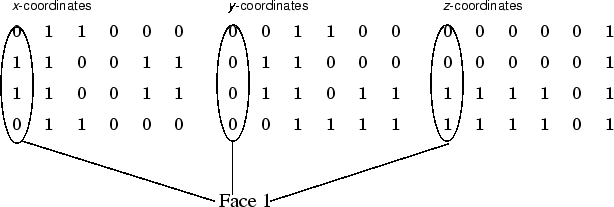
Каждый столбец матриц задает различную поверхность. В то время как существует только восемь вершин, необходимо задать 24 вершины, чтобы задать все шесть поверхностей. Поскольку каждая поверхность совместно использует вершины с четырьмя другими поверхностями, можно задать закрашенную фигуру более эффективно путем определения каждой вершины только однажды и затем определения порядка, в котором можно соединить эти вершины, чтобы сформировать каждую поверхность. Закрашенная фигура Vertices и Faces свойства задают закрашенные фигуры только этим способом.
Эти матрицы задают куб с помощью
Vertices и Faces.
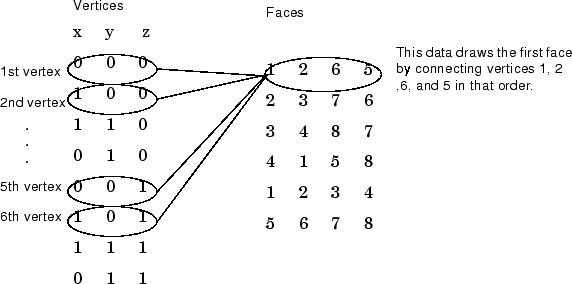
Используя вершины/поверхности метод может сохранить значительную сумму памяти компьютера, когда закрашенные фигуры содержат большое количество поверхностей. Этот метод требует формального patch синтаксис функций, который влечет за собой значения присвоения к Vertices и Faces свойства явным образом. Например,
patch('Vertices',vertex_matrix,'Faces',faces_matrix)
Поскольку высокоуровневый синтаксис автоматически не присваивает поверхность или цвета обводки, необходимо установить соответствующие свойства произвести закрашенные фигуры с цветами кроме белого цвета поверхности по умолчанию и черного цвета обводки.
Плоский цвет поверхности является результатом определения одного цвета на поверхность. Например, с помощью метода вершин/поверхностей и FaceVertexCData свойство задать цвет, этот оператор задает один цвет на поверхность и устанавливает FaceColor свойство к flat.
vert = [0 0 0;1 0 0;1 1 0;0 1 0;0 0 1;1 0 1;1 1 1;0 1 1];
fac = [1 2 6 5;2 3 7 6;3 4 8 7;4 1 5 8;1 2 3 4;5 6 7 8];
patch('Vertices',vert,'Faces',fac,...
'FaceVertexCData',hsv(6),'FaceColor','flat')
Настройте оси:
view(3) axis vis3d
Поскольку истинный цвет задан с FaceVertexCData свойство имеет тот же формат как палитра MATLAB (т.е. n-3 массив значений RGB), этот пример использует hsv палитра, чтобы сгенерировать шесть цветов, требуемых для закрашивания плоскостями.
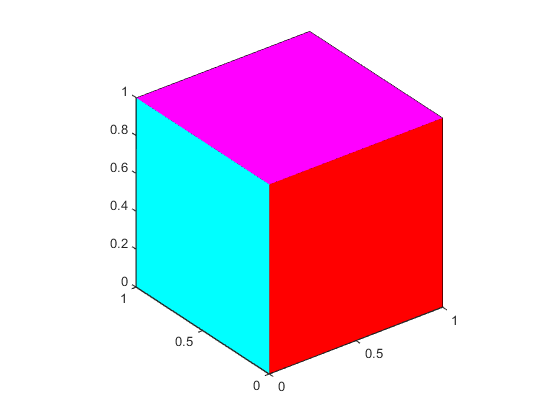
Чтобы сопоставить цвета поверхности с текущей палитрой, присвойте n-1 массив FaceVertexCData свойство:
patch('Vertices',vert,'Faces',fac,...
'FaceVertexCData',(1:6)','FaceColor','flat')Настройте оси:
view(3) axis vis3d
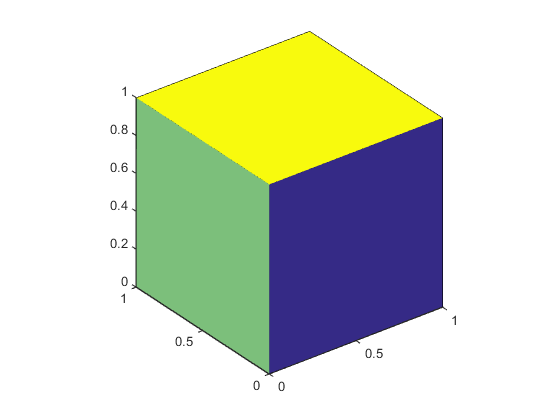
Интерполированный цвет поверхности означает, что цвета вершины каждой поверхности задают переход цвета от одной вершины до следующего. Чтобы интерполировать цвета между вершинами, необходимо задать цвет для каждой вершины и установить FaceColor свойство к interp.
patch('Vertices',vert,'Faces',fac,...
'FaceVertexCData',hsv(8),'FaceColor','interp')
Настройте оси:
view(3) axis vis3d
производит куб с каждой поверхностью, окрашенной путем интерполяции цветов вершины.
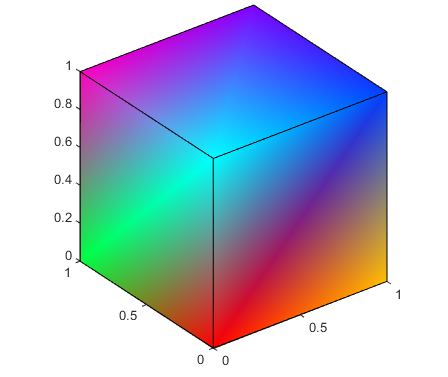
Чтобы задать ту же окраску с помощью x, y, z, c метод, c должен быть m n 3 массивами, где размерности x, y, и z являются m на n.
Эта схема показывает соответствие между FaceVertexCData и CData свойства.

То, как Данные о Закрашенной фигуре Относятся к Палитре, обсуждает окраску методов более подробно.