В этом примере показано, как сгенерировать и построить переднюю сторону Парето для 2D многоцелевой функции с помощью fgoalattain.
Эти две цели в этом примере переключены и масштабированные версии выпуклой функции .
function f = simple_mult(x)
f(:,1) = sqrt(1+x.^2);
f(:,2) = 4 + 2*sqrt(1+(x-1).^2);Оба компонента увеличиваются, как x уменьшается ниже 0 или увеличивается выше 1. Промежуточный 0 и 1, f 1 (x) увеличивается, и f 2 (x) уменьшается, таким образом, существует область компромисса.
t = linspace(-0.5,1.5); F = simple_mult(t); plot(t,F,'LineWidth',2) hold on plot([0,0],[0,8],'g--'); plot([1,1],[0,8],'g--'); plot([0,1],[1,6],'k.','MarkerSize',15); text(-0.25,1.5,'Minimum(f_1(x))') text(.75,5.5,'Minimum(f_2(x))') hold off legend('f_1(x)','f_2(x)') xlabel({'x';'Tradeoff region between the green lines'})
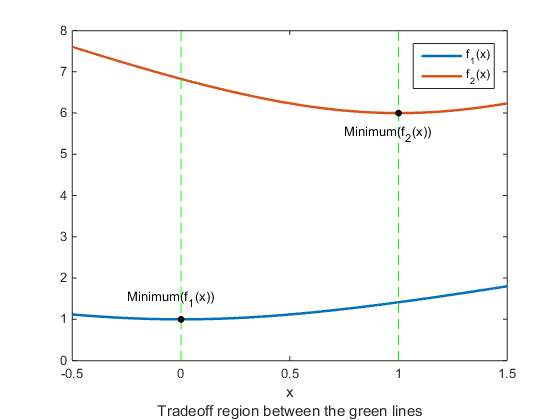
Чтобы найти переднюю сторону Парето, сначала найдите неограниченные минимумы двух функций. В этом случае вы видите контролем, что минимум f 1 (x) равняется 1, и минимум f 2 (x) равняется 6, но в целом вы можете должны быть использовать стандартную программу оптимизации.
В общем случае запишите функцию, которая возвращает конкретный компонент многоцелевой функции.
function z = pickindex(x,k) z = simple_mult(x); % evaluate both objectives z = z(k); % return objective k
Затем найдите минимум каждого компонента с помощью решателя оптимизации. Можно использовать fminbnd в этом случае, или fminunc для более многомерных проблем.
k = 1; [min1,minfn1] = fminbnd(@(x)pickindex(x,k),-1,2); k = 2; [min2,minfn2] = fminbnd(@(x)pickindex(x,k),-1,2);
Установите цели, которые являются неограниченным optima для каждого компонента. Можно одновременно достигнуть этих целей, только если многоцелевые функции не вмешиваются друг в друга, означая, что нет никакого компромисса.
goal = [minfn1,minfn2];
Чтобы вычислить переднюю сторону Парето, возьмите векторы веса [a, 1–a] для a от 0 до 1. Решите целевую задачу достижения, установив веса на различные значения.
nf = 2; % number of objective functions N = 50; % number of points for plotting onen = 1/N; x = zeros(N+1,1); f = zeros(N+1,nf); fun = @simple_mult; x0 = 0.5; options = optimoptions('fgoalattain','Display','off'); for r = 0:N t = onen*r; % 0 through 1 weight = [t,1-t]; [x(r+1,:),f(r+1,:)] = fgoalattain(fun,x0,goal,weight,... [],[],[],[],[],[],[],options); end figure plot(f(:,1),f(:,2),'k.'); xlabel('f_1') ylabel('f_2')

Вы видите компромисс между этими двумя целями.