Приложение оптимизации с решателем fmincon

В этом примере показано, как использовать приложение Оптимизации с fmincon решатель, чтобы минимизировать уравнение второй степени к линейным и нелинейным ограничениям и границам.

Примечание

Приложение Оптимизации предупреждает, что будет удалено в будущем релизе.

Считайте задачу нахождения [x ₁, x ₂], который решает

$\min_{x} f (x) = x_{}^{12} + x_{}^{22}$

удовлетворяющее ограничениям

$\begin{array}{r} 0.5 \leq x_{1} & (связанный) \\ - x_{1} - x_{2} + 1 \leq 0 & (линейное неравенство) \\ \begin{array}{r} - x_{}^{12} - x_{}^{22} + 1 \leq 0 \\ - 9 x_{}^{12} - x_{}^{22} + 9 \leq 0 \\ - x_{}^{12} + x_{2} \leq 0 \\ - x_{}^{22} + x_{1} \leq 0 \end{array}} & (нелинейное неравенство) \end{array}$

Начальным приближением для этой проблемы является x ₁ = 3 и x ₂ = 1.

Шаг 1: Запишите файл objecfun.m для целевой функции.

function f = objecfun(x)
f = x(1)^2 + x(2)^2;

Шаг 2: Запишите файл nonlconstr.m для нелинейных ограничений.

function [c,ceq] = nonlconstr(x)
c = [-x(1)^2 - x(2)^2 + 1;
     -9*x(1)^2 - x(2)^2 + 9;
     -x(1)^2 + x(2);
     -x(2)^2 + x(1)];
ceq = [];

Шаг 3: Настройте и запустите проблему с приложением Оптимизации.

Введите optimtool в Командном окне, чтобы открыть приложение Оптимизации.
Выберите fmincon от выбора решателей и изменения поле Algorithm к Active set.
Введите @objecfun в поле Objective function, чтобы вызвать objecfun.m файл.
Введите [3;1] в поле Start point.
Задайте ограничения.
- Установите связанный 0.5 ≤ x ₁ путем ввода [0.5,-Inf] в поле Lower. -Inf запись означает, что нет никакой нижней границы на x ₂.
- Установите линейное ограничение неравенства путем ввода [-1 -1] в поле A и вводят -1 в поле b.
- Установите нелинейные ограничения путем ввода @nonlconstr в поле Nonlinear constraint function.
В панели Options расширьте опцию Display to command window при необходимости и выберите Iterative показать информацию об алгоритме в Командном окне для каждой итерации.
Нажмите кнопку Start как показано в следующем рисунке.
Когда алгоритм останавливается под Run solver and view results, следующая информация отображена:
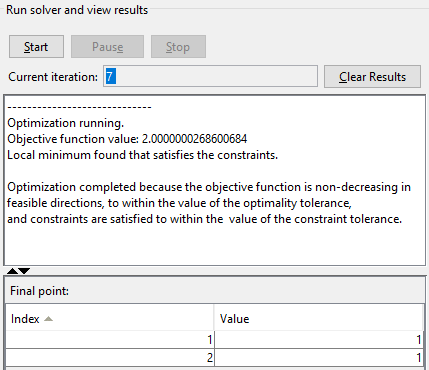
- Значение Current iteration, когда отключенный алгоритм, который для этого примера является 7.
- Окончательное значение целевой функции, когда алгоритм остановился:
```
Objective function value: 2.0000000268595803
```
- Сообщение завершения алгоритма:
```
Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the  value of the constraint tolerance.
```
- Конечная точка для этого примера является
```
    1
    1	
```

В Командном окне информация об алгоритме отображена для каждой итерации:

                                Max     Line search  Directional  First-order 
 Iter F-count        f(x)   constraint   steplength   derivative   optimality Procedure 
    0      3           10            2                                         Infeasible start point
    1      6      4.84298      -0.1322            1        -5.22         1.74   
    2      9       4.0251     -0.01168            1        -4.39         4.08  Hessian modified twice  
    3     12      2.42704     -0.03214            1        -3.85         1.09   
    4     15      2.03615    -0.004728            1        -3.04        0.995  Hessian modified twice  
    5     18      2.00033   -5.596e-05            1        -2.82       0.0664  Hessian modified twice  
    6     21            2   -5.326e-09            1        -2.81     0.000522  Hessian modified twice  
Active inequalities (to within options.ConstraintTolerance = 1e-06):
  lower      upper     ineqlin   ineqnonlin
                                     3
                                     4

Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the  value of the constraint tolerance.

Документация