Exponenta Banner

Уравнение Пуассона на единичном диске: приложение PDE Modeler

В этом примере показано, как решить уравнение Пуассона на единичном диске и оценить числовую ошибку решения.

Этот пример использует приложение PDE Modeler. Для программируемого рабочего процесса смотрите уравнение Пуассона на Единичном диске. Поскольку приложение и программируемый рабочий процесс используют различный meshers, они дают к немного отличающимся результатам.

Формулировка задачи является –Δu = 1 в Ω, u = 0 на ∂ Ω, где Ω является единичным диском. Точное решение

u(x,y)=1−x2−y24

Чтобы решить эту задачу в приложении PDE Modeler, выполните эти шаги:

  1. Откройте приложение PDE Modeler при помощи pdeModeler команда.

  2. Отобразите линии сетки путем выбора Options> Grid.

  3. Выровняйте новые формы к линиям сетки путем выбора Options> Snap.

  4. Нарисуйте круг с радиусом 1 и центр в (0,0). Для этого сначала нажмите кнопку. Затем щелкните правой кнопкой по источнику и перетащите, чтобы нарисовать круг. Щелчок правой кнопкой ограничивает форму, которую вы чертите так, чтобы это был круг, а не эллипс. Если круг не является совершенным модульным кругом, дважды кликните его. В получившемся диалоговом окне задайте точное центральное местоположение и радиус круга.

  5. Проверяйте, что режим приложения установлен в Generic Scalar.

  6. Задайте граничные условия. Для этого переключитесь на граничный режим путем нажатия кнопки или выбора Boundary> Boundary Mode. Выберите все контуры путем выбора Edit> Select All. Затем выберите Boundary> Specify Boundary Conditions и задайте граничное условие Дирихле u = 0. Это граничное условие является значением по умолчанию (h = 1, r = 0), таким образом, вы не должны изменять его.

  7. Задайте коэффициенты путем выбора PDE> PDE Specification или нажатия кнопки PDE на панели инструментов. Задайте c = 1, a = 0, и f = 1.

  8. Задайте максимальный размер ребра для mesh путем выбора Mesh> Parameters. Установите максимальный размер ребра на 0,1.

  9. Инициализируйте mesh путем выбора Mesh> Initialize Mesh или нажатия кнопки.

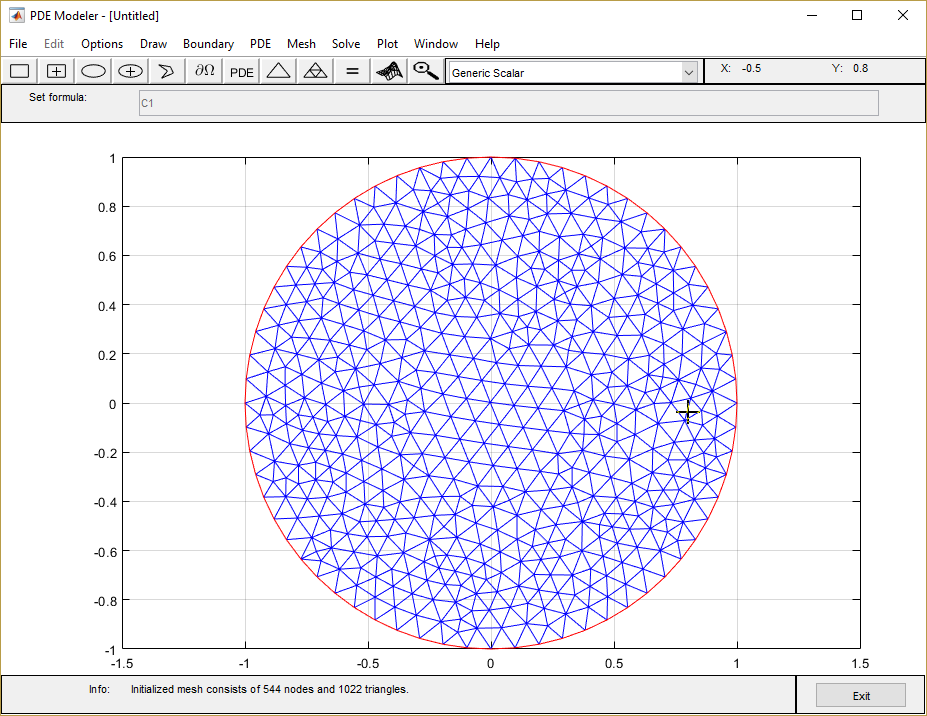
  10. Решите УЧП путем выбора Solve> Solve PDE или нажатия кнопки = на панели инструментов. Тулбокс собирает проблему УЧП, решает ее и строит решение.

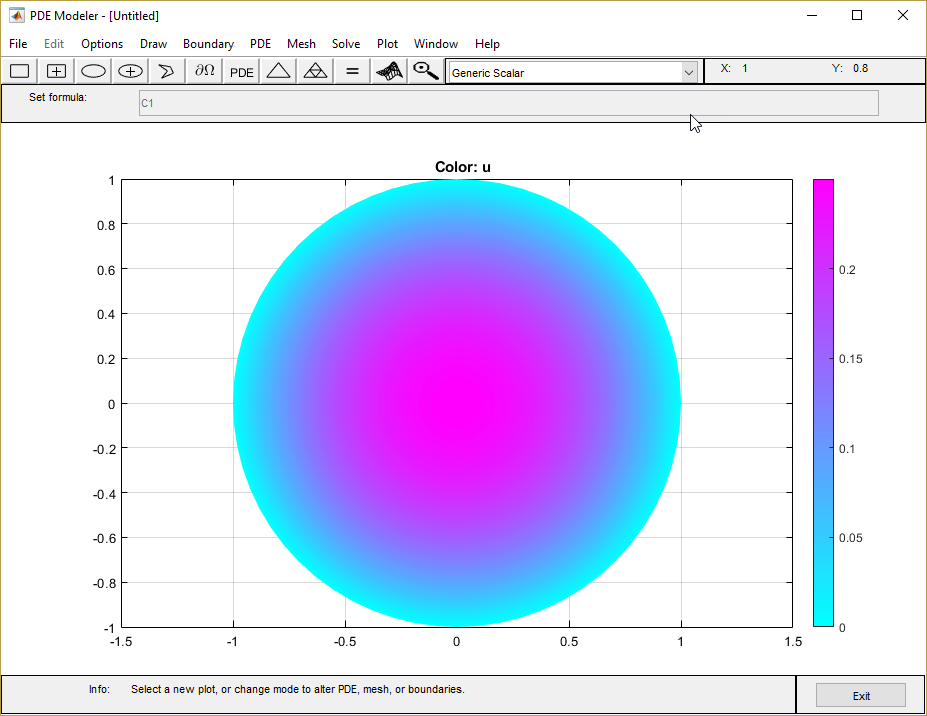
  11. Сравните числовое решение точного решения:

    1. Выберите Plot> Parameters.

    2. В получившемся диалоговом окне выберите user entry от Color выпадающее меню.

    3. Постройте абсолютную погрешность в решении путем ввода выражения MATLAB® u-(1-x.^2-y.^2)/4 в поле User entry.

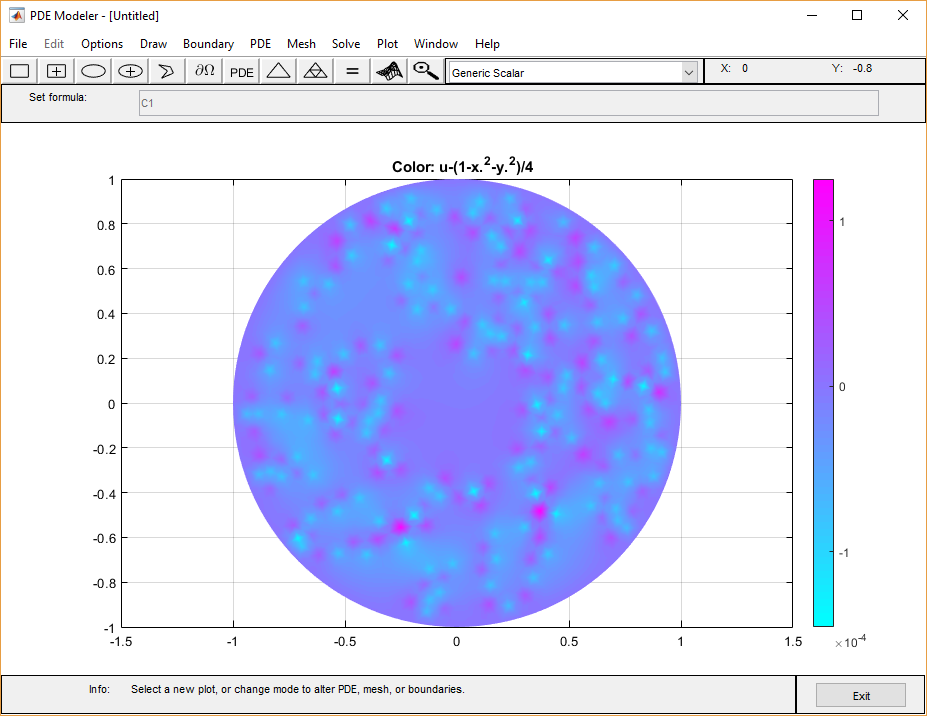
  12. Совершенствуйте mesh путем выбора Mesh> Refine Mesh или нажатия кнопки.

  13. Сравните числовое решение точного решения для усовершенствованной mesh. Постройте абсолютную погрешность.

  14. Экспортируйте данные о mesh и решение рабочего пространства MATLAB путем выбора Mesh> Export Mesh и Solve> Export Solution, соответственно.

Документация Partial Differential Equation Toolbox
Поддержка