Документация

Радарная концепция куба данных

Радарный куб данных является удобным способом концептуально представлять пространственно-временную обработку. Чтобы создать радарный куб данных, примите, что предварительная обработка преобразует сигналы РФ, полученные от нескольких импульсов через несколько элементов массива к основополосным выборкам с комплексным знаком. Расположите основополосные выборки с комплексным знаком в 3D массиве размера K-by-N-by-L.

Много радарных операций обработки сигналов в программном обеспечении Phased Array System Toolbox™ соответствуют обработке более низко-размерных подмножеств радарного куба данных. Подмножество могло быть одномерным подвектором или двумерной субматрицей.

Следующий рисунок показывает организацию радарного куба данных в этом программном обеспечении. Последующие разделы объясняют каждую из размерностей и какой аспект обработки пространства-времени они представляют.

Быстрые выборки времени

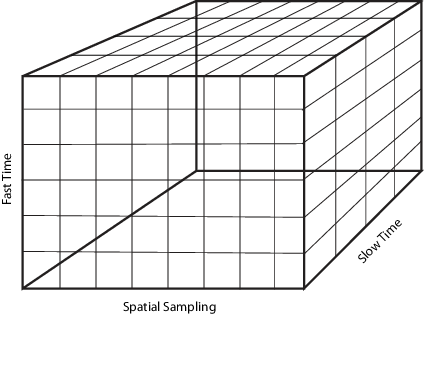
Считайте K-by-1 подвектором радарного куба данных вдоль быстро-разовой оси в вышеупомянутой схеме. Каждый вектор-столбец представляет набор основополосных выборок с комплексным знаком от одного импульса в одном элементе массива, произведенном на уровне$$F_s$$. Это - самый высокий уровень выборки системы и приводит к обозначению fast time. $$F_s$$ должен быть выбран, чтобы не искажать. Соответствующим интервалом выборки дают $$T_s=1/F_s$$. Быстрое измерение времени также упоминается как размерность области значений, и быстрые демонстрационные интервалы времени, когда преобразовано, чтобы дистанцировать использование скорости распространения сигнала, часто упоминаются как интервалы области значений или логические элементы области значений.

Импульсное сжатие является примером операции обработки сигналов, выполняемой на быстрых выборках времени. Другим примером обработки сигналов является dechirping. В этих типах операций количество выборок в первой размерности выхода может отличаться от входа.

Медленные выборки времени

Считайте каждый K-by-L субматрицей радарного куба данных. В каждой субматрице существуют векторы-строки K с размерностью 1 L. Каждый из этих векторов-строк содержит основополосные выборки с комплексным знаком от L различные импульсы, соответствующие тому же интервалу области значений. Существует K-by-L матрица для каждого из элементов массива N. Интервалом выборки между выборками L является pulse repetition interval (PRI). Типичные PRIs намного более длинны, чем быстро-разовый интервал выборки. Из-за долгих интервалов выборки выборки, взятые через несколько импульсов, упоминаются как slow time.

Обработка данных в медленно-разовой размерности позволяет вам оценивать Доплеровский спектр в данном интервале области значений. В этом типе операции может измениться количество выборок в третьей размерности куба данных. Количество Доплеровских интервалов не может совпасть с количеством импульсов.

Критерий Найквиста применяется одинаково к медленно-разовой размерности. Обратная величина PRI является импульсной частотой повторения (PRF). PRF дает ширину однозначного Доплеровского спектра.

Пространственная выборка

Поэтапные массивы состоят из нескольких элементов массива. Считайте каждый K-by-N субматрицей радарного куба данных. Каждый вектор-столбец состоит из K быстро-разовые выборки для одного импульса, полученного в элементе единого массива. Вектор-столбцы N представляют тот же импульс, произведенный через элементы массива N. Выборочные данные в вектор-столбцах N являются пространственной выборкой инцидентной формы волны. Анализ данных через элементы массива позволяет вам определить пространственное содержимое частоты каждого полученного импульса. Критерий Найквиста пространственной выборки требует, чтобы элементы массива не были разделены больше, чем половиной длины волны несущей частоты.

В пространственных операциях частоты может измениться количество выборок во втором измерении куба данных. Количество пространственных интервалов частоты не может совпасть с количеством элементов датчика.

Beamforming является пространственной операцией фильтрации, которая комбинирует данные через элементы массива, чтобы выборочно улучшить и подавить инцидент wavefields на массиве от конкретных направлений.

Пространственно-временная обработка

Space-time adaptive processing работает с двумерными данными углового Доплера для каждого интервала области значений. Считайте K-by-N-by-L радарным кубом данных. Каждая из выборок K является данными из той же области значений. Эта область значений производится через элементы массива N и L PRIs. Сворачивание 3D матрицы в каждом интервале области значений в N-by-L подматрицы позволяет одновременный двумерный анализ угла Доплеровской частоты и прибытия.

Организация данных в радарном кубе данных

Если у вас есть K основополосные выборки данных с комплексным знаком, собранные из импульсов L, полученных в датчиках N, можно организовать данные в формате, совместимом с соглашениями Phased Array System Toolbox с помощью permute. После обработки ваших данных, при необходимости можно преобразовать назад в исходный формат куба данных с ipermute.

origdata = randn(6,10,200)+1j*randn(6,10,200);

newdata = permute(origdata,[3 1 2]);

data = ipermute(newdata,[3 1 2]);