Детекторы Постоянного ложно-сигнального уровня (CFAR)

Ложный сигнальный уровень для детекторов CFAR

Открыть скрипт

В среде Неимен-Пирсона вероятность обнаружения максимизируется удовлетворяющая ограничению, что ложно-сигнальная вероятность не превышает заданный уровень. Ложно-сигнальная вероятность зависит от шумового отклонения. Поэтому, чтобы вычислить ложно-сигнальную вероятность, необходимо сначала оценить шумовое отклонение. Если шумовое отклонение изменяется, необходимо настроить порог, чтобы обеспечить постоянный ложно-сигнальный уровень. Постоянные ложно-сигнальные детекторы уровня реализуют адаптивные процедуры, которые позволяют вам обновить пороговый уровень своего теста, когда степень интерференции изменяется.

Чтобы мотивировать потребность в адаптивной процедуре, примите простой бинарный тест гипотезы, где необходимо решить между гипотезами сигнала существующими и сигнала отсутствующими для одной выборки. Сигнал имеет амплитуду 4, и шум является нулевым средним значением, гауссовым с модульным отклонением.

Во-первых, установите ложно-сигнальный уровень на 0,001 и определите порог.

T = npwgnthresh(1e-3,1,'real');
threshold = sqrt(db2pow(T))

threshold =

    3.0902

Проверяйте, что этот порог дает к желаемой ложно-сигнальной вероятности уровня, и затем вычислите вероятность обнаружения.

pfa = 0.5*erfc(threshold/sqrt(2))
pd = 0.5*erfc((threshold-4)/sqrt(2))

pfa =

   1.0000e-03


pd =

    0.8185

Затем примите, что шумовая степень увеличивается на 6,02 дБ, удваивая шумовое отклонение. Если ваш детектор не адаптируется к этому увеличению отклонения путем определения нового порога, ложно-сигнальные повышения ставки значительно.

pfa = 0.5*erfc(threshold/2)

pfa =

    0.0144

Следующий рисунок показывает эффект увеличения шумового отклонения на ложно-сигнальной вероятности для фиксированного порога.

noisevar = 1:0.1:10;
noisepower = 10*log10(noisevar);
pfa = 0.5*erfc(threshold./sqrt(2*noisevar));
semilogy(noisepower,pfa./1e-3)
grid on
title('Increase in P_{FA} due to Noise Variance')
ylabel('Increase in P_{FA} (Orders of Magnitude)')
xlabel('Noise Power Increase (dB)')

Составляющий в среднем ячейку детектор CFAR

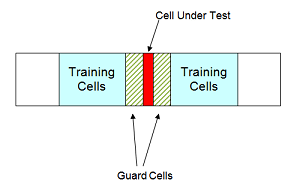
Составляющий в среднем ячейку детектор CFAR оценивает шумовое отклонение для ячейки области значений интереса или ячейки под тестом, путем анализа данных из соседних ячеек области значений, определяемых как учебные ячейки. Шумовые характеристики в учебных ячейках приняты, чтобы быть идентичными шумовым характеристикам в ячейке под тестом (CUT).

Это предположение является ключом в выравнивании по ширине использования учебных ячеек, чтобы оценить шумовое отклонение в CUT. Кроме того, составляющий в среднем ячейку детектор CFAR принимает, что учебные ячейки не содержат сигналов от целей. Таким образом данные в учебных ячейках состоят из шума только.

Сделать эти предположения реалистичными:

  • Желательно иметь некоторый буфер или guard cells, между CUT и учебными ячейками. Буфер, обеспеченный защитными ячейками, принимает меры против сигнала, просачивающегося в учебные ячейки и оказывающего негативное влияние на оценку шумового отклонения.

  • Учебные ячейки не должны представлять ячейки области значений, слишком удаленные в диапазоне от CUT, когда следующая фигура иллюстрирует.

Оптимальное средство оценки для шумового отклонения зависит от дистрибутивных предположений и типа детектора. Примите следующее:

  1. Вы используете квадратичный детектор.

  2. У вас есть Гауссова, случайная переменная (RV) с комплексным знаком с независимыми действительными и мнимыми частями.

  3. Действительные и мнимые части у каждого есть средний нуль и отклонение, равное σ2/2.

    Примечание

    Если вы обозначаете этот RV Z=U+jV, величина |Z|2 в квадрате следует за экспоненциальным распределением со средним значением σ2.

Если выборки в учебных ячейках являются величинами в квадрате такого комплексного Гауссова RVs, можно использовать демонстрационное среднее значение в качестве средства оценки шумового отклонения.

Чтобы реализовать составляющее в среднем ячейку обнаружение CFAR, используйте phased.CFARDetector. Можно настроить характеристики детектора, такие как количества учебных ячеек и охранять ячейки и вероятность ложного предупреждения.

Адаптация детектора CFAR к шумным входным данным

Скрипт Open Live Script

В этом примере показано, как создать детектор CFAR и протестировать его способность адаптироваться к статистике входных данных. Тест использует испытания только для шума. При помощи квадратичного детектора по умолчанию можно определить, как близко эмпирический ложно-сигнальный уровень к желаемой ложно-сигнальной вероятности.

Примечание: Этот пример запускается только в R2016b или позже. Если вы используете более ранний релиз, заменяете каждый вызов функции с эквивалентным step синтаксис. Например, замените myObject(x) с step(myObject,x).

Создайте объект детектора CFAR с двумя защитными ячейками, 20 учебными ячейками и ложно-сигнальной вероятностью 0,001. По умолчанию этот объект принимает квадратичный детектор без импульсного интегрирования.

detector = phased.CFARDetector('NumGuardCells',2,...
    'NumTrainingCells',20,'ProbabilityFalseAlarm',1e-3);

Существует 10 учебных ячеек и 1 защитная ячейка на каждой стороне ячейки под тестом (CUT). Установите индекс CUT на 12.

CUTidx = 12;

Отберите генератор случайных чисел для восстанавливаемого набора входных данных.

rng(1000);

Установите шумовое отклонение на 0,25. Это значение соответствует аппроксимированному ОСШ на-6 дБ. Сгенерируйте 23 10000 матрица белого Гауссова rv's с комплексным знаком с заданным отклонением. Каждая строка матрицы представляет 10 000 испытаний Монте-Карло за отдельную ячейку.

Ntrials = 1e4;
variance = 0.25;
Ncells = 23;
inputdata = sqrt(variance/2)*(randn(Ncells,Ntrials)+1j*randn(Ncells,Ntrials));

Поскольку пример реализует квадратичный детектор, возьмите величины элементов в квадрате в матрице данных.

Z = abs(inputdata).^2;

Обеспечьте выход от квадратичного оператора и индекса ячейки под тестом к детектору CFAR.

Z_detect = detector(Z,CUTidx);

Выход, Z_detect, логический вектор с 10 000 элементов. Суммируйте элементы в Z_detect и разделитесь на общее количество испытаний, чтобы получить эмпирический ложно-сигнальный уровень.

pfa = sum(Z_detect)/Ntrials
pfa = 0.0013

Эмпирический ложно-сигнальный уровень 0.0013, который соответствует тесно желаемому ложно-сигнальному уровню 0,001.

Расширения составляющего в среднем ячейку детектора CFAR

Составляющий в среднем ячейку алгоритм для детектора CFAR работает хорошо во многих ситуациях, но не всех. Например, когда цели тесно расположены, ячейка, составляющая в среднем, может заставить сильную цель маскировать слабую цель поблизости. phased.CFARDetector Система object™ поддерживает следующие алгоритмы обнаружения CFAR.

АлгоритмТипичное использование
Составляющий в среднем ячейку CFARБольшинство ситуаций
Самый большой - составляющего в среднем ячейку CFARКогда важно избежать, чтобы ложь предупредила в ребре помехи
Самый маленький - составляющего в среднем ячейку CFARКогда цели тесно расположены
Закажите статистический CFARПойдите на компромисс между самым большим - и самый маленький - усреднения ячейки

Вероятность обнаружения для детектора CFAR

Скрипт Open Live Script

В этом примере показано, как сравнить вероятность обнаружения, следующего из двух алгоритмов CFAR. В этом сценарии алгоритм статистической величины порядка обнаруживает цель, которую не делает составляющий в среднем ячейку алгоритм.

Примечание: Этот пример запускается только в R2016b или позже. Если вы используете более ранний релиз, заменяете каждый вызов функции с эквивалентным step синтаксис. Например, замените myObject(x) с step(myObject,x).

Создайте детектор CFAR, который использует составляющий в среднем ячейку алгоритм CFAR.

Ntraining = 10;
Nguard = 2;
Pfa_goal = 0.01;
detector = phased.CFARDetector('Method','CA',...
    'NumTrainingCells',Ntraining,'NumGuardCells',Nguard,...
    'ProbabilityFalseAlarm',Pfa_goal);

Детектор имеет 2 защитных ячейки, 10 учебных ячеек и ложно-сигнальную вероятность 0,01. Этот объект принимает квадратичный детектор без импульсного интегрирования.

Сгенерируйте вектор входных данных на основе белой Гауссовой случайной переменной с комплексным знаком.

Ncells = 23;
Ntrials = 100000;
inputdata = 1/sqrt(2)*(randn(Ncells,Ntrials) + ...
    1i*randn(Ncells,Ntrials));

Во входных данных замените строки 8 и 12, чтобы симулировать две цели для детектора CFAR, чтобы обнаружить.

inputdata(8,:) = 3*exp(1i*2*pi*rand);
inputdata(12,:) = 9*exp(1i*2*pi*rand);

Поскольку пример реализует квадратичный детектор, возьмите величины элементов в квадрате в векторе входных данных.

Z = abs(inputdata).^2;

Выполните обнаружение на строках 8 - 12.

Z_detect = detector(Z,8:12);

Z_detect матрица имеет пять строк. Первые и последние строки соответствуют симулированным целям. Три средних строки соответствуют шуму.

Вычислите вероятность обнаружения двух целей. Кроме того, оцените вероятность ложного предупреждения с помощью строк только для шума.

Pd_1 = sum(Z_detect(1,:))/Ntrials
Pd_1 = 0

Pd_2 = sum(Z_detect(end,:))/Ntrials
Pd_2 = 1

Pfa = max(sum(Z_detect(2:end-1,:),2)/Ntrials)
Pfa = 6.0000e-05

0 значение Pd_1 указывает, что этот детектор не обнаруживает первую цель.

Измените детектор CFAR, таким образом, он использует алгоритм CFAR статистической величины порядка с рангом 5.

release(detector);
detector.Method = 'OS';
detector.Rank = 5;

Повторите расчеты вероятности и обнаружение.

Z_detect = detector(Z,8:12);
Pd_1 = sum(Z_detect(1,:))/Ntrials
Pd_1 = 0.5820

Pd_2 = sum(Z_detect(end,:))/Ntrials
Pd_2 = 1

Pfa = max(sum(Z_detect(2:end-1,:),2)/Ntrials)
Pfa = 0.0066

Используя алгоритм статистической величины порядка вместо составляющего в среднем ячейку алгоритма, детектор обнаруживает первую цель приблизительно в 58% испытаний.

Документация Phased Array System Toolbox
Поддержка
Для просмотра документации необходимо авторизоваться на сайте