Прямоугольные координаты

Определения координат

Создайте прямоугольную, или Декартову, систему координат для 3-мерного пространства путем определения трех осей взаимно прямоугольной координаты. Следующий рисунок показывает одну возможную спецификацию осей координат.

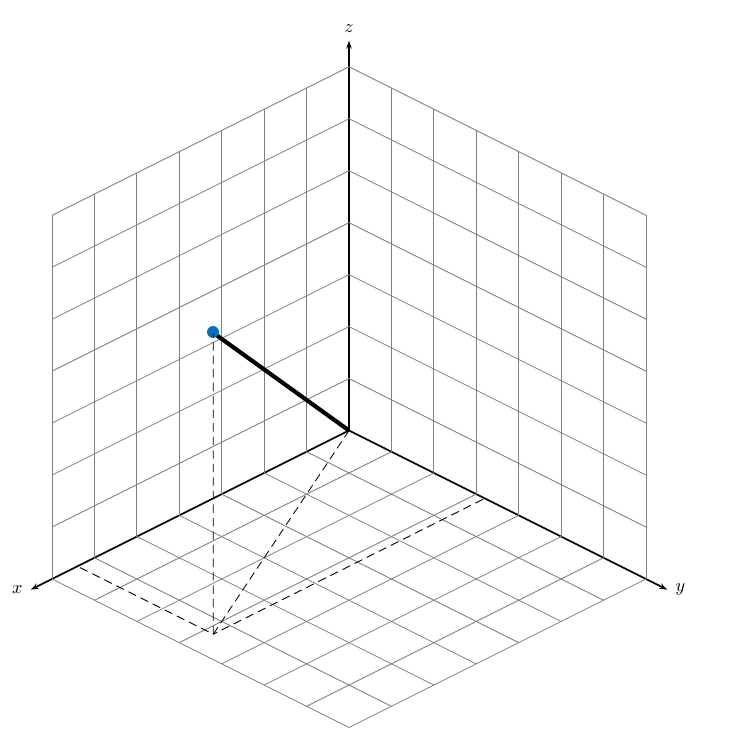
Прямоугольные координаты задают положение на пробеле в данной системе координат как упорядоченное с 3 кортежами из вещественных чисел, (x, y, z), относительно источника (0,0,0). Факторы для выбора источника обсуждены в Системах Глобальной и Локальной координаты.

Можно просмотреть с 3 кортежами как точку на пробеле, или эквивалентно как вектор в 3D Евклидово пространстве. Просматриваемый как векторное пространство, оси координат являются базисными векторами, и вектор дает направление точке на пробеле от источника. Каждый вектор на пробеле исключительно определяется линейной комбинацией базисных векторов. Наиболее распространенный набор базисных векторов для 3D Евклидово пространства является стандартными модульными базисными векторами:

${[1 0 0], [0 1 0], [0 0 1]}$

Обозначение для векторов и точек

В программном обеспечении Phased Array System Toolbox™ вы задаете и оси координат и точки как вектор-столбцы.

Примечание

В этом программном обеспечении все координатные векторы являются вектор-столбцами. Для удобства документация представляет вектор-столбцы в формате [x y z] без, транспонируют обозначение.

Оба векторное обозначение [x y z] и обозначение точки (x, y, z) используются взаимозаменяемо. Интерпретация вектор-столбца как вектор или точка зависит от контекста. Если вектор-столбец задает оси системы координат или направления, это - вектор. Если вектор-столбец задает координаты, это - точка.

Ортогональное основание и евклидова норма

Любые три линейно независимых вектора задают основание для 3-мерного пространства. Однако это программное обеспечение принимает, что базисные векторы, которые вы используете, являются ортогональными.

Стандартной мерой по расстоянию на пробеле является норма ^l2 или Евклидова норма. Евклидова норма вектора [x y z] задана:

$\sqrt{x^{2} + y^{2} + z^{2}}$

Евклидова норма дает длину вектора, измеренного от источника как гипотенуза прямоугольного треугольника. Расстояние между двумя векторами [_{x0 y0 z0}] и [_{x1 y1 z1}]:

$\sqrt{{(x_{0} - x_{1})}^{2} + {(y_{0} - y_{1})}^{2} + {(z_{0} - z_{1})}^{2}}$

Ориентация осей координат

Учитывая ортонормированный набор базисных векторов, представляющих оси координат, существует несколько способов ориентировать оси. Следующая фигура иллюстрирует одну такую ориентацию, названную правой системой координат. Стрелки на осях координат указывают на положительные направления.

Если вы берете правую руку и указываете его вдоль положительного x - оси с ладонью, стоящей перед положительным y - ось, и расширяете свой ползунок, ваш ползунок указывает на положительное направление z - ось.

Вращения и матрицы вращения

В преобразовании векторов в 3-мерном пространстве часто сталкиваются с матрицами вращения. Матрицы вращения используются в двух смыслах: они могут использоваться, чтобы вращать вектор в новое положение, или они могут использоваться, чтобы вращать координатное основание (или система координат) в новую. В этом случае вектор оставлен в покое, но его компоненты в новом основании будут отличаться от тех в исходном основании. В Евклидово пространстве существует три основных вращения: один каждый вокруг x, y и осей z. Каждое вращение задано углом вращения. Угол поворота задан, чтобы быть положительным для вращения, которое является против часовой стрелки, когда просматривается наблюдателем, смотрящим вдоль оси вращения на источник. Любое произвольное вращение может состоять из комбинации этих трех (теорема вращения Эйлера). Например, можно вращать вектор в любом направлении с помощью последовательности трех вращений: $v^{'} = A v = R_{z} (γ) R_{y} (β) R_{x} (α) v$ .

Матрицами вращения, которые вращают вектор вокруг x, y, и оси z, дают:

Против часовой стрелки вращение вокруг оси X

$R_{x} (α) = [\begin{matrix} 1000 & потому что α & - \sin α \\ 0 & \sin α & потому что α \end{matrix}]$
Против часовой стрелки вращение вокруг оси Y

$R_{y} (β) = [\begin{matrix} потому что β & 0 & \sin β \\ 010 \\ - \sin β & 0 & потому что β \end{matrix}]$
Против часовой стрелки вращение вокруг оси z

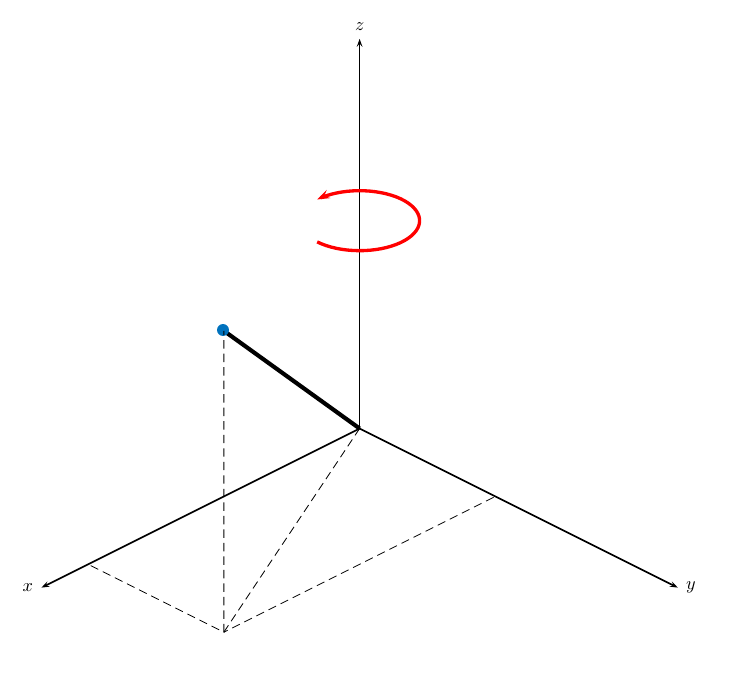
$R_{z} (γ) = [\begin{matrix} потому что γ & - \sin γ & 0 \\ \sin γ & потому что γ \\ 0001 \end{matrix}]$

Следующие три рисунка показывают то, на что положительные вращения похожи для каждой оси вращения:

Для любого вращения существует обратное удовлетворение вращения $A^{- 1} A = 1$ . Например, инверсия матрицы вращения оси X получена путем изменения знака угла:

$R_{x}^{- 1} (α) = R_{x} (- α) = [\begin{matrix} 1000 & потому что α & \sin α \\ 0 & - \sin α & потому что α \end{matrix}] = R_{x}^{'} (α)$

Этот пример иллюстрирует основное свойство: обратная матрица вращения является транспонированием оригинала. Матрицы вращения удовлетворяют A’A = 1, и следовательно det(A) = 1. При вращениях длины вектора сохраняются, а также углы между векторами.

Мы можем думать о вращениях в другом отношении. Рассмотрите исходный набор базисных векторов, $i, j, k$ , и вращайте их всех использование матрицы вращения A. Это производит новый набор базисных векторов $i^{'}, j,^{'} k^{'}$ связанный с оригиналом:

$\begin{array}{l} i^{'} & = A i \\ j^{'} & = A j \\ k^{'} & = A k \end{array}$

Используя транспонирование, можно записать новые базисные векторы как линейные комбинации старых базисных векторов:

$[\begin{matrix} i^{'} \\ j^{'} \\ k^{'} \end{matrix}] = A^{'} [\begin{matrix} i \\ j \\ k \end{matrix}]$

Теперь любой вектор может быть записан как линейная комбинация любого набора базисных векторов:

$v = v_{x} i + v_{y} j + v_{z} k = {v^{'}}_{x} i^{'} + {v^{'}}_{y} j^{'} + {v^{'}}_{z} k^{'}$

Используя алгебраическую манипуляцию, можно вывести преобразование компонентов для фиксированного вектора, когда основание (или система координат) вращается. Это преобразование использует транспонирование матрицы вращения.

$[\begin{matrix} {v^{'}}_{x} \\ {v^{'}}_{y} \\ {v^{'}}_{z} \end{matrix}] = A^{- 1} [\begin{matrix} v_{x} \\ v_{y} \\ v_{z} \end{matrix}] = A^{'} [\begin{matrix} v_{x} \\ v_{y} \\ v_{z} \end{matrix}]$

Следующая фигура иллюстрирует, как вектор преобразовывается, когда система координат вращается вокруг оси X. Рисунок после показывает, как это преобразование может быть интерпретировано как вращение вектора в противоположном направлении.

Документация